Coefficient de Dissymétrie
SPSS
![]()

Estimateur de dissymétrie
Pearson 2
![]()

Indice D
Duncan & Duncan [1955]
![]()

Indice D(adj)
Morrill [1991]
![]()

Indice d'autocorrélation spatiale
I de Moran
![]()
![]()
Indice de ségrégation
Schelling
![]()
Ces pages sont le résultat d'un travail dans le cadre du Master of Arts de la Faculté des Lettres de l'Université de Lausanne, section Géographie. Il a été réalisé en 2004 et présente l'état de ségrégation spatiale de la population dite "étrangère" dans les principales villes Suisses, se basant sur les données hectométriques du Recensement Fédéral de la Population 1990. J'ai consacré d'autres études à la ségrégation urbaine, à cette époque, produisant notamment un modèle basé agents de la ségrégation socio-spatiale, qui peut être consulté ailleurs sur mon site. - André Ourednik, PhD, 2012
Le présent site propose une exploration quantitative du phénomène de ségrégation spatiale de la population des étrangers dans quatorze villes suisses. Pour chaque unité spatiale traitée, un taux d'étrangers a été établi et, pour chaque ville, des indices de ségrégation ont été calculés.
Des cartes locales de la répartition de la population étrangère peuvent être accédées au travers de la carte nationale ou par le menu. Le menu permet également d'accéder aux cartes comparatives des taux de ségrégation des villes, en fonction de l'indice de mesure.
Chaque carte comparative est accompagnée d'une explicitation mathématique complète de l'indice utilisé. Le script Mathematica utilisé pour calculer des indices plus complexes est également disponible pour téléchargement. Le site se propose ainsi, comme but secondaire, d'explorer les indices de ségrégation eux-mêmes dans leur adéquation au problème traité et dans leur capacité de rendre compte des patterns spatiaux observables à l'œil nu sur les cartes locales.
Les définitions, la signification sociale, la méthode et les observations générales du travail ayant conduit à l'existence du présent site sont présentés en détail dans ce qui suit.
La ségrégation peut être définie comme un processus (et son résultat) de division sociale et spatiale d'une société en unités distinctes [1].
Ces unités consistent en agrégats d'individus similaires qui, par leur mouvement d'assemblement, augmentent leur distance – spatiale ou sociale – à d'autres individus et à d'autres agrégats. De ce fait découle que la ségrégation a pour pendant un mouvement d'agrégation. Les termes renvoient néanmoins à des phénomènes divergents. Alors que l' agrégation relève d'un acte de libre choix, la notion de ségrégation revoie à une exclusion imposée, s'exprimant le plus clairement dans un déni actif ou passif d'accès à certains biens ou prestations dont le reste de la société, ou certaines de ses couches, disposent.
Pour un géographe, la ségrégation a deux formes. Elle s'exprime à la fois socialement et spatialement.
Ceux qui la subissent peuvent, d'une part, être les exclus sociaux dont la ségrégation n'est liée à aucun lieu. Ils la portent avec eux en tout temps et tout lieu, en étant les seuls corrélats – étant eux-mêmes des ségrégés, des marginaux. La ségrégation qu'ils subissent ne consiste pas en un accès limité à l'espace mais en leur vécu involontairement partiel de l'ensemble de l'espace social.
D'autre part, l'espace d'une société lui même peut être polarisé. Bien qu'il serait exagéré de parler de ghettos dans le cadre des villes suisses, généralement trop peu étendues, il est possible d'y observer et de mesurer une inhomogénéité de la structure de la population sur l'étendue de l'espace. C'est précisément cette inhomogénéité qui est étudiée dans le présent site.
La ségrégation, nous l'avons vu plus haut, n'est pas nécessairement un phénomène entièrement néfaste. Dans sa forme agrégative, volontaire, nous connaissons les enclaves ethniques que constitue parfois une minorité urbaine "lui permettant, par les relations particulières entre employeurs et employés appartenant à la même communauté ethnique, d'assurer une bonne performance économique aux premiers et un meilleur accès au marché du travail aux seconds" [1].
Mais même l'avantage de ce type d'agrégation est discutable du point de vue de l'ensemble de la société. Parce que la ville n'est pas une simple "projection sur le sol des rapports sociaux" [2] – elle est ces "rapports", au même titre que n'importe quel autre phénomène de collectivité. Cela signifie que, de manière générale, alors même qu'elle présenterait des avantages relatifs pour une population restreinte, la ségrégation spatiale a pour corollaire le morcellement de la société. " La proximité spatiale ne garantit pas la proximité sociale mais on est en droit de penser que la distance spatiale renforce à coup sur la distance sociale " [3]. Ainsi, la ségrégation spatiale entraîne logiquement un manque d'identification, donc de solidarité et de collaboration entre les groupes qu'elle contribue à constituer. Ce manque de solidarité peut prendre la forme de la méfiance, de la xénophobie ou, carrément, de la franche hostilité mutuelle. Même ce qui semblerait un avantage localisé devient ainsi un désavantage global pour tout groupe social.
D'autre part, le manque de cohésion spatiale constitue une entrave au fonctionnement d'organisations globales. Ainsi, par exemple, la ségrégation spatiale aux États-unis a largement contribué à empêcher l'émergence d'une classe ouvrière capable de défendre ses droits [4].
Dans le cas des étrangers dans les villes suisses, et avec ce qui précède, il convient de comprendre les taux de ségrégation présentés dans ce travail comme autant de signes d'incapacité des structures politiques d'intégrer une tranche de la population – 20.9% en 1990, pour l'ensemble des villes étudiées – dans la vie collective. Incapacité, d'une part, d'offrir aux populations étrangers et suisses des moyens et structures d'échange qui conduirait les deux populations à reconnaître l'une l'autre en tant que participante d'une même société et qui éviterait, à l'une comme à l'autre, la nécessité de se retrancher dans des espaces urbains circonscrits. Incapacité, d'autre part, d'imposer une politique d'aménagement urbain intégrative aux acteurs privés de l'immobilier et des transports.
Dans des cités d'aujourd'hui, multiculturelles et en polarisation constante, le rôle de l'Etat devrait être celui d'un constant effort d'homogénéisation de la répartition de la population dans l'espace habité, dans le but de permettre le tissage de liens culturels entre les citadins de diverses origines. Les indicateurs présentés dans ce travail espèrent pouvoir identifier les villes suisses où un tel effort n'avait pas été suffisamment fourni.
Le recensement de la population 1990 de l'OFS couvre l'ensemble de la population suisse. Partiellement pour des raisons techniques, liées à la capacité encore très limitée des ordinateurs actuels de gérer des bases de données de grande taille, nous avons cependant restreint notre analyse à quatorze villes particulières. Notre choix s'est porté sur celles des villes suisses dont les quartiers sont référenciés comme unités territoriales standard de l'OFS. Ceci nous empêche de prendre en considération certaines agglomérations urbaines dans toute leur étendue mais nous permet de disposer d'un maillage territorial prédéfini qui, de plus est, correspond au maillage de l'intervention administrative des communes les plus importantes de la Suisse.
Pour chaque ville prise à part, nous utilisons comme maillage d'analyse le découpage hectométrique de l'OFS. Les unités de 100x100 mètres résultant de ce découpage constituent nos individus géoréférencées dont la ségrégation est calculée. Chacun d'entre aux est caractérisé par une paire de coordonnées et par un taux d'étrangers. Afin que les taux calculés soient significatifs, nous avons éliminé du calcul toute unité ayant moins de dix habitants.
Le choix des indicateurs a été fait en mesure du but de l'analyse et de la nature des données.
Afin, d'abord, de rendre compte de l'inhomogénéité de la distribution de la population étrangère dans l'espace, nous avons fait usage de deux indicateurs de l'écart à la distribution normale que sont le coefficient de dissymétrie et le deuxième estimateur de dissymétrie de Pearson. Dans le même but, nous avons également fait usage du fréquemment utilisé indice de ségrégation D de Duncan & Duncan. Etant donnée que ces trois indices ne prennent pas en considération la localisation des unités spatiales mais les traitent comme entités abstraites, certains auteurs les appellent aspatiaux . Ils relèvent ainsi le fait qu'aucun de ces indices n'est capable de refléter la réalité de l'échange entre les diverses unités spatiales.
Afin de remédier à ce manque, un grand nombre d'indicateurs dits spatiaux ont été inventés. Certains d'entre eux, très sophistiqués, dépassent même les nécessités de notre étude. Il en est ainsi de tous les indices prenant en compte la forme et les dimensions des unités spatiales, comme par exemple l'indice D(w) de Wong qui attribue un poids d'interaction aux paires d'unités spatiales en fonction de la longueur de leur frontière commune. Etant donné que nos unités spatiales sont le produit d'un maillage hectométrique régulier, de telles précisions sont superflues dans notre cas.
Néanmoins, la localisation spatiale de nos unités nous intéresse. Pour cette raison, nous avons fait usage de trois des indicateurs dits spatiaux. Le premier d'entre eux est l'indice D(adj) de Morrill qui soustrait à l'indice D le degré d'interaction potentielle entre les suisses et les étrangers au travers des frontières des unités spatiales voisines. Le deuxième est le souvent présenté coefficient d'autocorrélation spatiale de Moran. Notre troisième indicateur répartit et rend compte de leur exposition mutuelle. Etant donné qu'il s'agit là d'une formalisation que nous avons faite d'une mesure de ségrégation proposée par Schelling dans son fréquemment cité "Micromotives and Macrobehaviour", nous le nommons indice de Schelling.
Du à la masse de calculs impliquée par la computation de ces trois indices, il n'ont pas été calculés pour les villes de Basel, Bern et Zürich, qui englobent un trop grand nombre d'unités spatiales.
Une description plus détaillée de chaque indicateur peut être accédée par le menu.
Les observations liées aux indices particuliers sont exposées dans les descriptions de ces indices. Néanmoins les remarques générales suivantes peuvent être faites par rapport à l'ensemble des observations:
D'une part, les trois indices "alocalisés", ainsi que l'indice D(adj) enregistrent une ségrégation plus élevée dans les villes du Nord-Est du pays, c'est-à-dire, dans les villes alémaniques. D'autre part, nous remarquons que les indices de ségrégation "localisés" tendent à être plus élevés dans les villes à plus grande superficie.
Sur les cartes à grandes échelle consacrées aux villes particulières, nous observons également que là où des patterns de ségrégation sont décelables, la population des étrangers tend à ce concentrer en centre ville et le long des axes de communication principaux, plutôt qu'en périphérie. Nous pouvons expliquer ce fait d'une part par la proximité des moyens de transport [5]. La population étrangère, en effet, ne dispose souvent pas de moyens de transport personnel. Ceci l'empêche de suivre l'exode urbain qui entraîne ceux qui le peuvent en direction des périphéries champêtres [6]. L'une des raisons de cet exode étant la fuite de l'autre – et particulièrement la fuite de l'étranger – il n'est pas étonnant de trouver des taux d'étrangers élevés dans ce qui était le cœur des villes.
Parmi les critiques générales les plus importantes sur la nature des valeurs obtenues nous relevons que nous ne savons pas qui sont les étrangers pris en compte. L'origine et la culture des étrangers joue en réalité un rôle majeur dans l'importance des barrières qui s'érigent entre ceux-ci et la population suisse. La ségrégation des délégués internationaux à Genève n'est pas la même que celle des requérants d'asile à Thun. Ne pas connaître et ne pas prendre en compte ces données met en doute certaines observations qui ont pu être faites avec la seule aide des indices utilisés dans l'élaboration de ce site
D'autre part, nous voulons remarquer que les valeurs obtenues ne permettent pas de rendre compte de l'effort de déségrégation des villes qui naturalisent une grande partie de leur population étrangère. De telles villes pourraient montrer des taux de ségrégation particulièrement hauts (même si nous doutons du fait que la ségrégation des étrangers à Thun ou Schaffhausen vient du fait de trop nombreuses naturalisations). Nous notons cela car la naturalisation des étrangers suisses, bien plus encore que leur répartition homogène dans l'espace urbain nous semble la condition d'une véritable reconnaissance mutuelle et de l'éveil d'une conscience d'appartenance à une société commune. Cette conscience nous paraît absolument nécessaire à l'élaboration de l'avenir d'une société et d'un pays.
[1] Brunet, Ferras, Théry [1992] Preticeille [1995], 9
[2] H. Lefèbvre, cité par Preticeille [1995].
[3] Preticeille [1995] d'après CHAMBORODON J. C., LEMAIRE M. [1970] "Proximité spatiale et distance sociale: les grands ensembles et leur peuplement". Revue française de sociologie , XI, 1.
[4] Selon la thèse de Ira Katynelson [1981], mentionnée par Preticeille [1995], 11.
[5] Racine [2001]
[6] Pumain, Sanders, Saint-Julien [1989], 8
Coefficient de Dissymétrie
SPSS
![]()

Estimateur de dissymétrie
Pearson 2
![]()

Indice D
Duncan & Duncan [1955]
![]()

Indice D(adj)
Morrill [1991]
![]()

Indice d'autocorrélation spatiale
I de Moran
![]()
![]()
Indice de ségrégation
Schelling
![]()
Bavaud F. [1998] Modèles et données: Une intoduction à la statistique uni-, bi- et trivariée. Paris: L'Harmattan.
Bégin J. Mesure de dissymétrie: Le coefficient de dissymétrie. From: http://www.er.uqam.ca/nobel/r30574/PSY1300/C3P11.html
Benenson I., Omer I. [2002] "Measuring individual segregation in space - A formal approach and case study" In: Schnell I., Ostendorf W. (eds.) Studies in Segregation and Desegregation Burlington:Ashgate. p. 11-38.
Brunet R., Ferras R., Théry H. [1992] Les mots de la géographie, dictionnaire critique. Montpellier-Paris: Reclus.
Cividjian A. V. Modèles Statisques et Fiabilité. From: http://elth.ucv.ro/nou3/cividjian/modele%20statistice%20si%20fiabilitate.pdf
Janda K. Summary statistics: Measures of dispersion. From: http://www.janda.org/c10/Lectures/topic03/L11-dispersion/L11-Dispersion.html
Oberi M. [1995] "L'analyse localisée de la ségrégation urbaine: ville, quartiers et cités dans une commune de la banlieue parisienne" In: Sociétés Contemporaines. 22/23, p. 127-143.
Preteceille E. [1995] Ségrégations urbaines In: Sociétés Contemporaines. 22/23, p. 5-14.
Racine J.-B. [2002] "Migration, Places and Intercultural Relations in Cities" In: Schnell I., Ostendorf W. (eds.) Studies in Segregation and Desegregation Burlington:Ashgate. p. 67-86.
Rhein C. [1994] "La ségrégation et ses mesures" In: Brun, Rhein (eds.) La ségrégation dans la ville. Paris: L'Harmattan, p. 121-161.
Schelling T. C. [1969] “Models of Segregation” In: American Economic Review: Papers and Proceedings. 59(2): p. 488-493.
Schelling T. C. [1971] “Dynamic Models of Segregation” In: Journal of mathematical sociology. 1, 143-186.
Schelling T. C. [1978] Micromotives and Macrobehavior. New York, London: Norton.
Tabard N. [1993] "Des quartiers pauvres aux banlieues aisées: une représentation sociale du territoire" In: Economie et Statistique. 270, p. 5-22.
Weisstein E. W. "Skewness" In: MathWorld – A Wolfram Web Ressource From: http://mathworld.wolfram.com/Skewness.html
Wong D.W.S. [2003] "Implementing spatial segregation measures in GIS" In: Computers, Environment and urban Systems. 27(2003): p. 53-57.
Le coefficient de dissymétrie (skewness) fait partie du package standard de SPSS. Le software utilise, pour le calculer, la formule suivante:
![]()
avec:

Un résultat différent de zéro montre qu' dissymétrie existe, et le signe permet de déterminer de quel type de dissymétrie il s'agit. Pour a 3 > 0 on a une dissymétrie positive étalée à droite. Pour a 3 < 0 on a une dissymétrie négative étalée à gauche. [ Figure 1 ]. Remarquons que le principe de cet indice réside dans le fait que les valeurs des écarts à la moyenne sont élevées à la puissance 3 avant d'être cumulées, ce qui permet à la fois de conserver le signe de l'écart et donner un poids exponentiellement élevé aux écarts importants. L'unité de l'indice est l'écart-type, élevé lui même à la puissance 3, afin de produire des résultats intuitivement interprétables.

Figure 1 : Distribution normale avec une dissymétrie positive , nulle et négative.
Comme il est possible de le voir sur la carte, la valeur moyenne de l'indice de dissymétrie des villes traitées monte à 1.43 et s'étend de 0.23 pour Genève à 3.09 (!) pour Thun. Cela représente un étalement à droite considérable de la distribution du taux des étrangers dans la majorité des villes.
Nous pouvons en déduire qu'alors qu'une majorité des unités spatiales contient un taux d'étrangers peu élevé, une minorité d'entre elles abrite un taux d'étrangers important. Cette minorité est même extrêmement faible pour certaines villes comme Thun ou Coire. Les étrangers, dans ces villes sont spatialement confinés dans quelques unités spatiales.
L'indice de dissymétrie ne permet cependant pas de dire si ces unités spatiales sont elles-mêmes isolées du reste de la ville par confinement dans un quartier particulier.
Pour avoir de plus amples détails sur la distribution du taux des étrangers , il est possible de se rapporter aux histogrammes accessibles en cliquant sur les villes appropriées.
La dissymétrie dite de Pearson vaut (a3)². Pearson a cependant également défini d'autres estimateurs de dissymétrie, en termes de variables plus intuitives que sont la moyenne, le mode et la médiane d'une distribution. Ces indices sont basés sur la réflexion suivante:
Lorsqu'une distribution est symétrique, sa moyenne, sa médiane et son mode sont équivalents. Lorsqu'elle ne l'est pas, ces valeurs divergent – la moyenne s'écarte de la médiane et du mode, et cela dans le sens de l'étalement de la distribution [Figure 2].
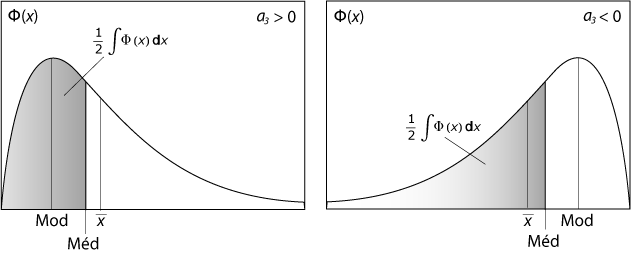
Figure 2 : Dissymétrie positive et négative en termes de mode, médiane et moyenne pour deux distributions Φ(x).
Par conséquent, il est possible de définir la dissymétrie en fonction de l'écart entre ces valeurs, que l'on exprime en termes d'écart-type, s , afin de remédier aux variations dues aux changements d'échelle.
Nous obtenons ainsi d'abord le premier coefficient de dissymétrie de Pearson exprimé par la formule suivante:
![]()
Mod(x) représente ici le mode. Le grand désavantage de l'estimateur Pearson1 est la difficulté de son application à des distributions polymodales. Pour remédier à ce problème il est possible d'utiliser un autre indicateur appelé deuxième coefficient de dissymétrie de Pearson que l'on peut exprimer par la formule suivante:
![]()
avec:
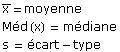
Le facteur 3, qui multiplie la différence entre la moyenne et le mode, est présent pour rendre compte de l'observation empirique suivante:
![]()
La mesure gagne ainsi en caractère intuitif en rendant approximativement compte de la distance entre le point maximum d'une distribution et sa moyenne.
Pour avoir de plus amples détails sur la distribution du taux des étrangers , il est possible de se rapporter aux histogrammes accessibles en cliquant sur les villes appropriées.
Comme il est possible de voir sur la carte, la valeur moyenne de l'estimateur de dissymétrie des villes traitées monte à 0.660 et s'étend de 0.14 pour Genève à 0.95 pour Schaffhausen. Cela signifie que la moyenne des taux d'étrangers de toutes les villes est supérieure à la valeur la plus fréquentes. Cela parfois de façon importante, notamment pour les villes de Schaffhausen, de Bâle et de St-Gallen.
Nous pouvons en déduire qu'une faible nombre d'unités spatiales a un taux d'étrangers élevé au point de tirer la moyenne locale vers le haut. Cela laisse croire que les étrangers, dans ces villes, sont spatialement confinés dans quelques unités spatiales.
L'estimateur de dissymétrie Pearson2 ne permet cependant pas de dire si ces unités spatiales sont elles-mêmes isolées du reste de la ville par confinement dans un quartier particulier.
Dans son ouvrage "Models in segregation ", Schelling [1978] propose plusieurs façons de calculer la ségrégation de deux populations réparties dans l'espace. L'une de ces façons est de calculer le rapport entre le nombre de voisins similaires et le nombre de voisins total pour tous les individus. C'est ainsi que nous définissons un indice de ségrégation que nous nommons "indice de Schelling". Formellement, nous choisissons de l'exprimer ainsi:
![]()
avec:
![]()
![]()
![]()
![]()
![]()
Comme l'indique la formule, nous avons fixé 142 mètres comme seuil de proximité nécessaire à l'interaction. Ceci définit l'interaction le voisinage de chaque unité spatiale de la manière suivante:
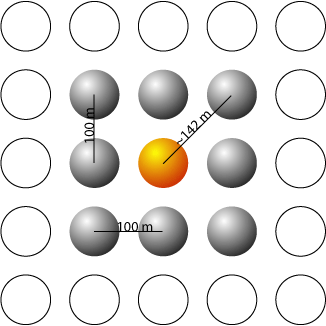
Comme seuil pour les valeurs binaires ξ, nous assignons soit le troisième quartile national, soit le troisième quartile local (propre à une ville particulière) du taux de ségrégation des étrangers. Dans les deux cas, nous obtenons deux populations distinctes pour lesquelles nous pouvons mesurer un taux d'exposition mutuelle – un taux mesuré en termes de la proportion de voisins différents aux nombre de voisins total pour chaque unité spatiale.
Lorsque le seuil est local, l'indice de Schelling reflète l'exposition d'une population aux lieux pouvant être perçus comme domaines de l'autre population au sein d'une ville.
Lorsque le seuil est global, l'indice de Schelling reflète l'exposition d'une population aux lieux pouvant être objectivement considérés comme domaines de l'autre population.
Parce que l 'indice de Schelling ne permet pas de rendre compte de la manière dont la ségrégation spatiale est instanciée, il est possible de considérer les cartes à plus grande échelle accessibles en cliquant sur les villes appropriées. Un schéma de coloration a été appliqué pour refléter graphiquement la répartition des populations selon les deux types de seuils. Pour identifier de figures de ségrégation , il est donc possible de mettre à profit la perception optique humaine qu'aucun algorithme ne peut véritablement égaler, sauf s'il s'agit de comparer de façon objectivable ces figures entre elles.
Du point de vue local, la ségrégation est la plus importante à St-Gallen, où 73.5% de voisins en moyenne sont similaires à l'unité centrale d'un voisinage. Ce qui est frappant est que Genève aussi fait preuve d'un haut taux de ségrégation (72%), alors que cette ville est identifiée comme la moins ségrégée par la plupart des autres indicateurs. De manière encore plus étonnante, Genève fait également preuve d'une haute ségrégation du point de vue plus objectif du seuil global. Ce deuxième fait s'explique cependant, car le taux d'étrangers à Genève est tel que la majorité des unités spatiales peuvent être considérées comme domaine de l'étranger – elles n'ont quasiment pas de voisins "suisses" est restent donc "parmi elles"; ceci se reflète sur le taux de ségrégation. Du point de vue local, la ville la moins est Fribourg avec, tout de même, 66.3% de voisins similaires en moyenne.
Du point de vue global, c'est Thun qui enregistre le taux de ségrégation le plus élevé, avec 89.2% de voisins similaires en moyenne pour toute unité centrale d'un voisinage. Ce taux contraste étonnamment avec l'un des taux de ségrégation les plus bas du point de vue local. Alors qu'elle fait preuve du taux d'étrangers le plus bas du pays, il est donc possible que les habitants de Thun perçoivent leur ville comme intégrative. Le taux de ségrégation du point de vue global est le plus bas é Neuchâtel et à Lausanne avec 60.4% et 60.8% de voisins similaires respectivement.
L'indice D de Duncan & Duncan est l'une des mesures la plus communes de ségrégation spatiale. Nous remercions David W. Wong de l'Université de Buffalo pour avoir mis à disposition son script Avenue permettant d'obtenir les valeurs de cet indice directement dans ArcView, en utilisant les données Arc/shape livrées par l'OFS.
L'indice D peut être calculé de la manière suivante:
![]()

Il mesure l'homogénéité (evenness) de la distribution de deux groupes de population dans l'espace et enregistre les écarts à cette homogénéité. Contrairement aux indices de dissymétrie, il n'opère pas avec des taux mais directement avec le nombre d'individus dans chaque unité spatiale. Par conséquent, il ne mesure pas la normalité de la distribution d'une population dans l'espace mais le degré de l' exposition mutuelle de deux groupes, comparé à un maximum d'exposition possible que représenterait leur distribution homogène. Sa valeur vaut zéro dans le cas d'une distribution homogène des deux populations. A chaque fois que, dans une unité spatiale, une population est surreprésentée par rapport à l'autre, la somme finale est incrémentée de la différence entre leur représentations locales. Cette somme est souvent divisée par deux.
Le défaut de l'indice D, pourtant fréquemment utilisé en géographie, est le fait qu'il ne considère pas la distribution spatiale des populations. Comme les indices de dissymétrie, il ne prend pas en compte les coordonnées des unités spatiales. Leur possible interaction par-delà leurs frontières et l'atténuation de la ségrégation qu'elle implique pour des unités voisines n'est ainsi pas prise en considération.
Les plus hautes valeurs de l'indice D peuvent être observées dans les villes de Thun et de Schaffhausen. Dans ces villes, les deux groupes sont le moins exposés l'un à l'autre, du moins du point de vue de leur occupation d'unités spatiales prises individuellement.
Le coefficient généralisé de Moran, le plus souvent appelé "I de Moran" est, dans notre cas, la différence entre la variance pondérée du taux d'étrangers et la variance locale généralisée du même taux, exprimée en termes de la variance pondérée. Il exprime la corrélation entre le taux d'étrangers à un endroit donné et les taux d'étrangers des unités spatiales voisines. Formellement, le I de Moran peut être exprimé de la manière suivante:
![]()
avec:
![]()
![]()
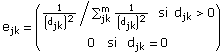
![]()
![]()
Comme on peut le voir, le taux d'interaction entre les unités spatiales, conservé dans la matrice des interactions, e , a été défini en tant que l'inverse du carré de la distance. Comme unité d'interaction, nous avons choisi la somme des interactions totale. Ceci signifie que la somme des poids statistiques des unités spatiales est de 1, ce qui simplifie l'interprétation des valeurs obtenues. (Nous reconnaissons que cette façon de définir les interactions n'est pas optimale. L'espace de la géographie humaine n'est pas un espace géométrique cartésien et il serait, en effet, préférable de définir les interactions en fonction des flux de personnes et de communications entre les diverses unités. Les données nécessaires à cette fin ne nous étaient cependant pas disponibles.)
L'avantage de l'indice I de Moran est, dans notre cas, le fait que le taux d'étrangers de chaque lieu est considéré en relation aux taux de l'ensemble des unités spatiales d'une ville, même si les interactions deviennent asymptotiquement nulles pour des grandes distances.
Plus la valeur de l'indice s'écarte de zéro, plus il y a de corrélation entre les unités spatialement proches, ce qui est le signe de l'existence d'un pattern spatial – un pattern de ségrégation dans notre cas.
Remarquons qu'une autocorrélation peut être négative, signifiant que les unités spatiales les plus proches présentent les taux les plus divergents. Ceci n'est cependant pas le cas pour l'autocorrélation du taux d'étrangers dans les villes suisses.
Parce que l 'indice de Moran est ne permet pas de rendre compte de la forme des patterns dont la présence est mesurée, il est nécessaire de se rapporter aux cartes à plus grande échelle accessibles en cliquant sur les villes appropriées.
Toutes les valeurs du I de Moran observées sont positives, bien que légèrement. La plus haute d'entre elles a été enregistrée pour St-Gallen. Dans cette ville, il existe donc la forme la plus clairement délimitée d'un arrangement spatial de la résidence des étrangers; la nationalité y joue un rôle dans le choix (ou de la possibilité de choix) de logement. Un I de Moran relativement élevé peut également être observé à Lausanne et Genève, villes présentant des valeurs peu élevées pour la majorité des autres indices. Fribourg et de Thun présentent un I de Moran extrêmement bas (0.08 dans les deux cas), ce qui signifie que quasiment aucun pattern n'est observable. Coire également, présente un I de Moran très bas. Remarquons que même en théorie, avec une matrice d'interaction telle que nous l'avons définie ici, il serait impossible de créer un pattern dont résulterait une autocorrélation négative; une autocorrélation de zéro est le minimum atteignable. Nous pouvons donc dire qu'à Fribourg, à Thun et à Coire, la nationalité ne détermine pas la région de la ville où habite un individu. Ce propos doit cependant être atténué par le fait que la superficie de ces trois villes ne permet simplement pas d'y déterminer des régions particulières. Généralement, les villes peu étendues présentent une autocorrélation basse, vu qu'un pattern de ségrégation n'y a pas la place de se former.
L'indice D(adj) de Morrill correspond à l'indice D auquel on aura soustrait une valeur correspondant au degré d'interaction potentielle entre les deux groupes au travers des frontières des unités spatiales. Ce degré est mesuré par la somme des différences des taux entre des unités voisines. En effet, plus cette comme est élevée, plus il y a d'interaction entre des unités spatiales à taux d'étrangers divergents. Ceci implique une exposition mutuelle des suisses et des étrangers non prise en compte par l'indice D.
L'indice D(adj) peut être exprimé de la manière suivante:
![]()
avec:
![]()

Comme l'indique la formule, nous avons fixé 142 mètres comme seuil de proximité nécessaire à l'interaction. Ceci définit l'interaction en termes d'un voisinage pouvant être représenté de la manière suivante:

Le désavantage de l'indice D(adj), tel qu'il est exprimé ici, réside dans le fait que sa représentation du voisinage se limite aux unités spatiales immédiatement adjacentes à l'unité traitée. Il n'est pas tenu compte de l'interaction entre unités distantes de plus de 142 mètres ; alors que nous pouvons supposer que même par-delà cette distance, une interaction existe, même si elle est moindre.
La prise en compte du voisinage dans la mesure de la ségrégation a pour effet l'atténuation de la différence entre les taux de ségrégation des villes observées. Cette atténuation peut néanmoins avoir pour seule cause l'exclusion de trois villes du calcul.
Malgré la diminution du taux de ségrégation par rapport à l'indice D, Schaffhausen et Thun demeurent les villes où la population suisse et étrangère sont relativement peu exposées l'une à l'autre. D'autre part, la diminution dans la ville de Luzern est peu importante, au point que cette ville se classe de côté de Schaffhausen et de Thun, du point de vue de la non-exposition mutuelle des deux populations dans un périmètre de 142 mètres.
L'indice D(adj) ne nous permet cependant pas de dire si les taux de ségrégation de ces villes resteraient relativement élevés, alors que nous prendrions en considération le potentiel d'interaction de toutes leurs unités spatiales avec toutes les autres.