Cet exercice fait suite à l’exercice Visualiser des données avec R (1). Il présuppose que vous avez chargé les données et créé les variables de cet exercice précédent, faute de quoi les scripts R ci-dessous ne fonctionneront pas. Les commentaires du code sont minimaux. Cet exercice présuppose soit, 1. que vous venez de suivre une séance de mon cours dédiée à l’introduction aux sur les réductions dimensionnelles à l’Université de Neuchâtel ou 2., que vous maîtrisez déjà les concepts sous-jacents.
Notez également que ce tutoriel ne prend en compte que les techniques liées aux anaylses en composantes principales et au clustering ascendant hiérarchique. Pour étudier des méthodes non-linéaires comme UMAP ou tSNE, rendez-vous plutôt ici.
De 1 dimension à 0 dimensions: le nombre unique qui résume les données
Réduisons d’abord nos données en un seul point, en réduisant une série de nombres en un seul nombre. Un nombre unique peut, en effet, être considéré comme un point dépourvu de dimension.
Moyenne, écart type, corrélation etc.
summary(langues$germanophones)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 0.00000 0.09091 0.78918 0.58595 0.92976 1.00000
sd(langues$germanophones) # écart-type des germanophones
# 0.3965477
sd(langues$germanophones)/mean(langues$germanophones) # variance des germanophonnes
# 0.6767584
cor.test(langues$germanophones, langues$francophones) # test de corrélation entre la proportion de francophones et de germanophones
# Pearson's product-moment correlation
#
# data: langues$germanophones and langues$francophones
# t = -87.391, df = 2768, p-value < 2.2e-16
# alternative hypothesis: true correlation is not equal to 0
# 95 percent confidence interval:
# -0.866326 -0.846491
# sample estimates:
# cor
# -0.8567249Code language: R (r)Comme on pouvait s’y attendre, il y a une corrélation négative significative à alpha < 0.00001 entre le proportion de francophones et de germanophones en Suisse.
Test du Chi2
Ce petit exemple se base sur des données catégorielles fictives que l’on crée dans un premier temps. Ensuite on obtient la p-value du Chi2.
voting <- cbind(
c(rep("Femme",600), rep("Homme",400)),
c(rep("Republican",250),rep("Democrat",300),rep("Independent",50),rep("Republican",200),rep("Democrat",150),rep("Independent",50))
)
colnames(voting) <- c("Genre","Parti")
tbl = table (voting[,1],voting[,2]) # construct contingency table from raw data
tbl
addmargins(tbl)
chisq.test(tbl)
# X-squared = 16.204, df = 2, p-value = 0.000303 -> selon la p value, il est à 99% sur qu'il y un lien entre sexe et parti
ct <- chisq.test(tbl, rescale.p = TRUE)
ct$expectedCode language: R (r)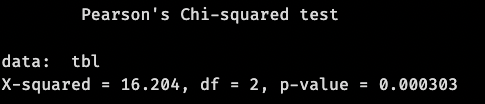
Le résultat montre que l’hypothèse H0 – selon laquelle la différence entre les votes des hommes et les votes des femmes serait due à des variations aléatoires – peut être rejetée avec une probabilité d’erreur alpha < 0.1 %.
De n dimensions à 2 dimensions
De nombreuses techniques de réduction dimensionnelle existent aujourd’hui. Les exemples ci-dessous se concentrent sur la méthode de l’analyse en composantes principales.
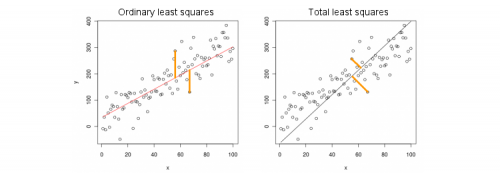
Lignes et surfaces de régression
Il existe des régressions ordinaires et des régressions orthogonales. Voici quelques régressions ordinaires en 3 dimensions:
# surface simple
splot <- scatterplot3d(langues.scaled$germanophones,langues.scaled$francophones,langues.scaled$italophones,xlab="germanophones",ylab="francophones",zlab="italophones",type="h",color="blue")
regression.plane <- lm(langues.scaled$germanophones ~ langues.scaled$francophones+langues.scaled$italophones)
splot$plane3d(regression.plane)Code language: R (r)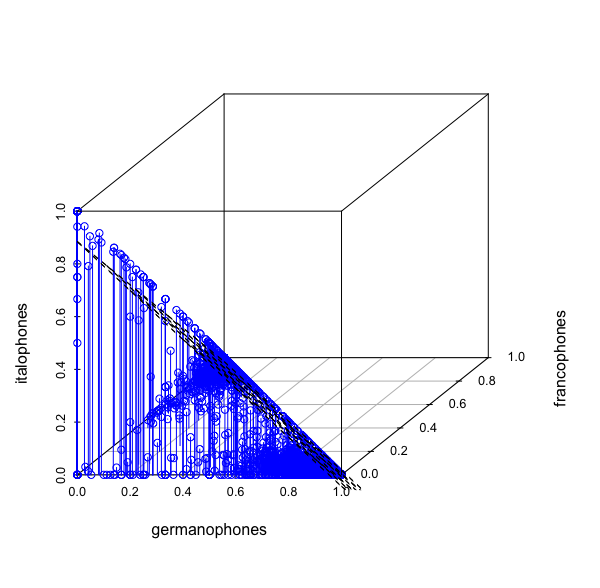
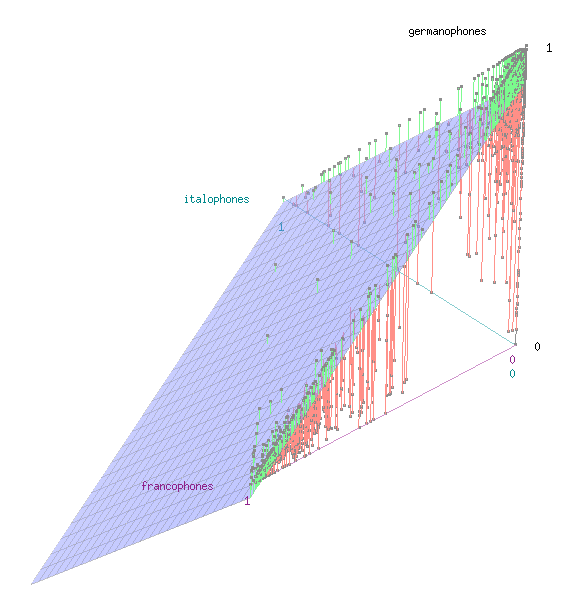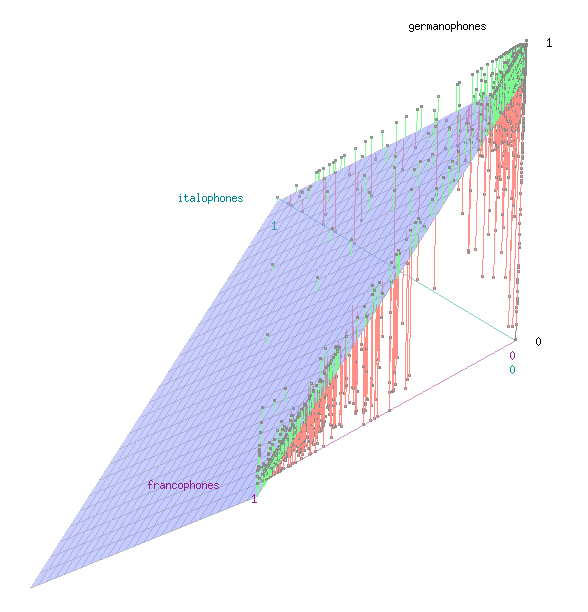
D’autres surface peuvent également être dessinées à l’aide du module car.
library(car)
scatter3d(germanophones ~ francophones + italophones, data=langues.scaled[,1:3],surface=F, point.col="black")
scatter3d(germanophones ~ francophones + italophones, data=langues.scaled[,1:3],fit="linear", point.col="black")
scatter3d(germanophones ~ francophones + italophones, data=langues.scaled[,1:3],fit="quadratic", point.col="black")Code language: R (r)Analyse en composantes principales
pc2.langues <- prcomp(langues.scaled)
eigen3d1 <- pc2.langues$rotation[1:3,1]
eigen3d2 <- pc2.langues$rotation[1:3,2]
eigen3d3 <- pc2.langues$rotation[1:3,3]
center <- pc2.langues$center
biplot(pc2.langues,expand=3,xlim=c(-0.1,0.1),ylim=c(-0.1,0.1)) # with labels
biplot(pc2.langues,expand=2,xlim=c(-0.05,0.05),ylim=c(-0.05,0.15),xlabs=rep("●", nrow(langues.scaled))) # only dots
Code language: R (r)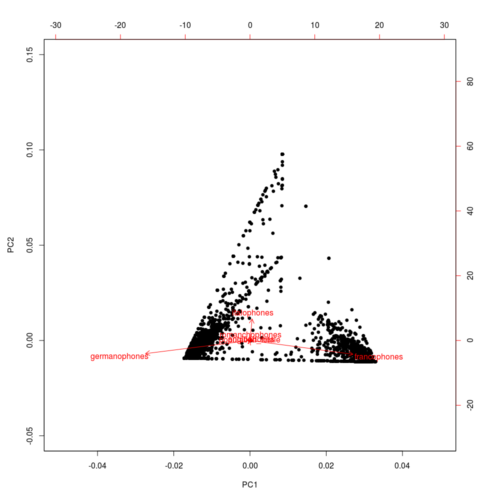
# fitting the projection planewith eigenvectors
spheres3d(langues.scaled$germanophones,langues.scaled$francophones,langues.scaled$italophones,radius=0.01,color="blue")
axes3d()
title3d(xlab="germanophones",ylab="francophones",zlab="italophones")
#Render the plane. NB: when you plot a plane using planes3d(a, b, c, d, alpha=0.5), you are effectively saying "Plot a point for every x, y and z that satisfies this equation.": a x + b y + c z + d = 0. Therefore d=-(ax+by+cz), and xyz should be the center of my plot. Moreover, abc are coordinates of the NORMAL to the desired plane, which is the third eigenvector in our case (we want the firts two dimensions). It doesn't totally work with prcomp. There is an imprecision, the eigenvectors are not perfectly orthogonal (if they were the crossproduct would be 0):
a = eigen3d3[1]
b = eigen3d3[2]
c = eigen3d3[2]
d = -(a*center[1]+b*center[2]+c*center[3])
planes3d(a,b,c,d, alpha=0.4)Code language: R (r)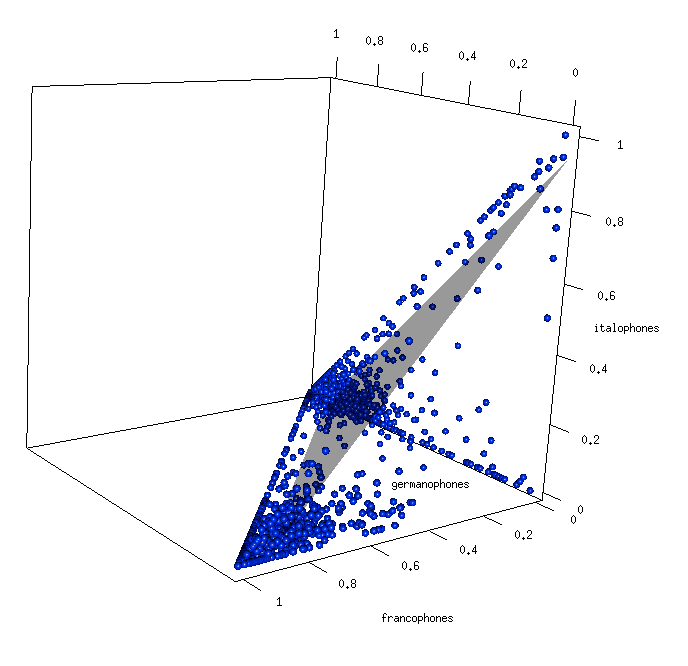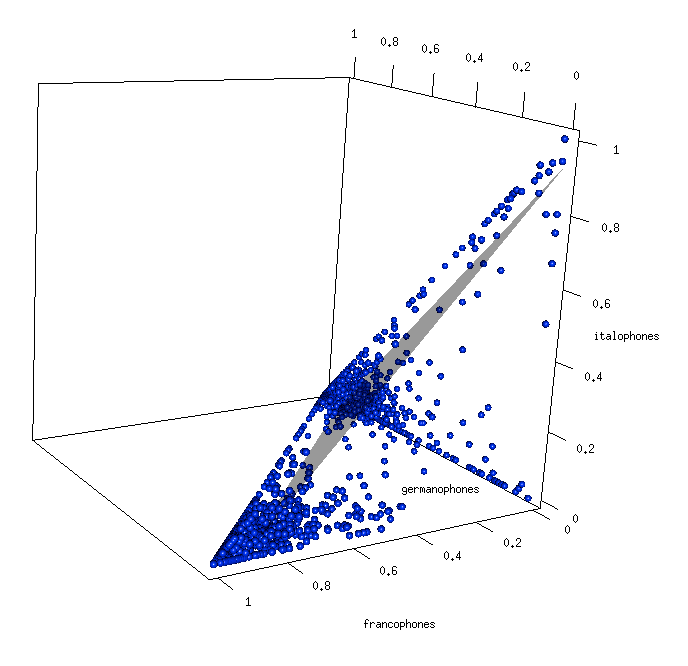
Clustering ascendant hiérarchique
d <- dist(as.matrix(langues.scaled))
hc <- hclust(d)
library("ggdendro")
ggdendrogram(hc, rotate = FALSE, size = 2)Code language: R (r)Pour voir le résultat, cliquez sur l’image ci-dessous.

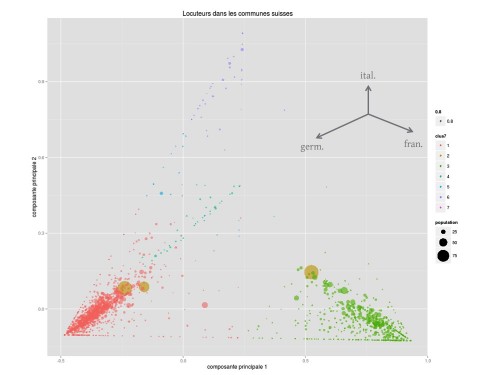
Combiner le clustering et l’analyse en composantes principales
Utiliser les clusters obtens comme couleurs pour la visualisation finale de l’analyse en composantes principales
groups <- as.data.frame(as.character(cutree(hc,7)))
colnames(groups) <- c("clus7")
pc1 <- pc2.langues$x[,1] # luckily the PCA coordinates results are also in the same order as original data
pc2 <- pc2.langues$x[,2]
langues.groups <- cbind(langues,pc1,pc2,groups)
ggplot(langues.groups, aes(x=pc1, y=pc2)) +
geom_point(aes(size=population_totale^(0.5),color=clus7,alpha=0.8)) +
scale_size_continuous(range = c(1,15),name="population") +
xlab("composante principale 1") +
ylab("composante principale 2") +
ggtitle("Locuteurs dans les communes suisses")Code language: R (r)