Une “série temporelle” est une suite d’enregistrements d’une variable faits au cours du temps. Cette variable peut être la température, la fréquence d’accidents routiers ou l’amplitude du son enregistré par un microphone. Les mesures peuvent être prises à des intervalles réguliers ou pas.
Pour avoir une base de discussion, préparons d’abord quelques données fictives. Ne vous inquiétez pas si vous ne comprenez pas l’extrait de code suivant, sa conception ne fait pas partie des objectifs du présent tutoriel; il génère simplement des données que nous pourrons analyser par la suite à l’aide de diverses méthodes.
t = 0:299
set.seed(100) # pour rendre l'exemple reproductible
y_stationary <- rnorm(length(t),mean=0.5,sd=0.08)
y_trend <- cumsum(rnorm(length(t),mean=1,sd=6))
y_trend <- y_trend/max(y_trend)
y_stationary_cyclic <- sin(t/5) + rnorm(length(t),mean=2,sd=0.3)
y_stationary_cyclic <- y_stationary_cyclic/max(y_stationary_cyclic)
d <- (sin(t/20) + 1)
y_stationary_cyclic_irreg <- sin(t/(4.5+d*0.4)) + rnorm(length(t),mean=2,sd=0.3)
y_stationary_cyclic_irreg <- y_stationary_cyclic_irreg/max(y_stationary_cyclic_irreg)
y_trend_cyclic <- sin(t/5) * 20 + cumsum(rnorm(length(t),mean=1,sd=2.5))
y_trend_cyclic <- y_trend_cyclic/max(y_trend_cyclic)Code language: R (r)Visualisons ces cinq séries:
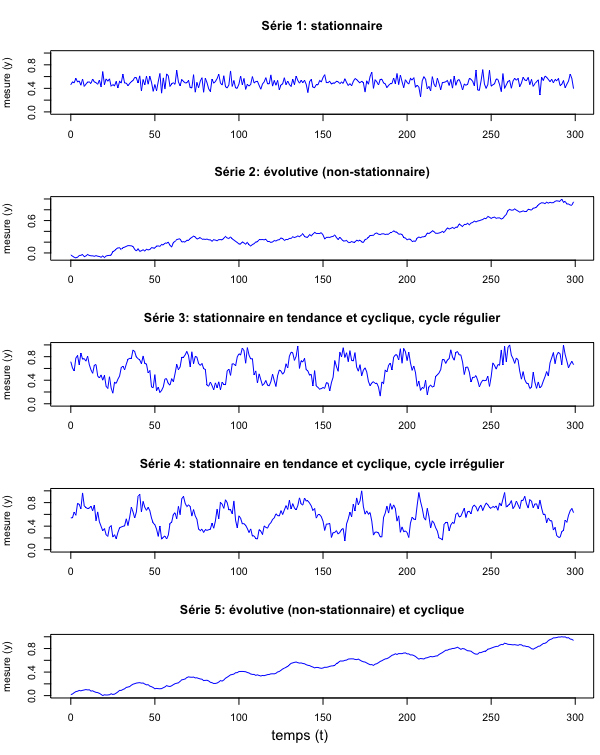
Comme vous le voyez, une série temporelle peut être stationnaire ou évolutive. Elle peut aussi être cyclique ou acyclique. Il y a même des séries cycliques évolutives. La durée d’un cycle s’appelle une fréquence. Les cycles peuvent être plus ou moins complexes, voire chaotiques.
En musique, lorsque plusieurs cycles réguliers, possédant chacun une fréquence distincte, se superposent, nous entendons un accord musical. Il en est de même dans de nombreux domaines de l’existence: des cycles de fréquences diverses liés à des phénomènes divers se superposent et s’enchevêtrent. En science, nous cherchons souvent à déchevêtrer les cycles complexes pour comprendre, un par un, les cycles réguliers qui les composent. Des méthodes mathématiques aident en cela. Les algorithmes prédéfinis dans R et dans ses modules par des mathématiciennes expérimentées permettent d’appliquer ces méthodes sans en maîtriser toutes les subtilités mathématiques.
Tester des hypothèses
En observant une série temporelle, le scientifique cherchera à défendre une hypothèse portant sur le phénomène qu’elle mesure. Ce phénomène s’amplifie-t-il avec le temps? Est-il cyclique ou acyclique? Est-il régulier? Les mathématiques proposent des tests permettant de vérifier de telles hypothèses.
Stationnaire ou évolutive?
D’habitude, on veut d’abord savoir si un phénomène augmente ou diminue avec le temps. La fréquence des feux de forêt augmente-t-elle avec les années? La surmortalité liée à la malaria diminue-t-elle? En termes statistiques, cela équivaut à tester la non-stationnarité d’une série temporelle.
L’approche avec un test de corrélation linéaire générique, et ses pièges épistémologiques
Souvent, les chercheurs abordent cette tâche en vérifiant s’il existe une corrélation linéaire entre le temps et la valeur de la mesure; ils testent surtout la significativité de cette corrélation. Voici la formule du coefficient de corrélation de Pearson (rty) utilisée dans ces cas, et que je vous invite à ne pas regarder si les formalismes mathématiques vous découragent, vu que la suite de ce tutoriel n’exige pas de la comprendre dans le détail.
Pour ce qui est du test du coefficient de corrélation, comme dans la plupart des tests statistiques, il s’agit de calculer la probabilité que la fluctuation des valeurs avec le temps soit due au pur hasard. Si cette probabilité est faible, on peut “rejeter l’hypothèse nulle” et considérer que la valeur de la mesure et le temps sont corrélés; autrement dit que la série est non-stationnaire. Cette approche n’est pas fausse en soi, si l’on se rappelle ce que “corrélation” veut dire en s’aidant de la figure suivante:
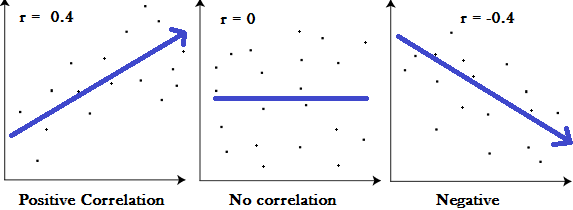
En apparence, il suffit de mettre le temps sur l’abscisse pour faire de la corrélation une mesure de non-stationnarité. Essayons à l’aide de la fonction cor.test() qui calcule la corrélation de Pearson. Appliquons-la à notre “série 1” que nous savons stationnaire:
cor.test(t,y_stationary) Code language: CSS (css)Résultat:
Pearson's product-moment correlation
data: t and y_stationary
t = 0.37969, df = 298, p-value = 0.7044
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.09147885 0.13489471
sample estimates:
cor
0.02198978 Les deux valeurs importantes de ce résultat sont la corrélation (2.2%) et sa p-value (70.4%). Remarquez qu’ici comme dans la suite de ce tutoriel, je convertis directement les nombres décimaux en pourcents pour une meilleure lisibilité. Le test nous dit en outre qu’il y a 95% de chances que la “véritable corrélation” entre temps et valeur soit comprise dans “l’intervalle de confiance” entre -9% et 13%. Notez que 0% est un nombre inclus dans cette fourchette: en d’autres mots, il se pourrait très bien que valeur et temps ne soient pas du tout corrélés. En bref, l’algorithme détecte une légère corrélation mais avertit qu’elle est probablement due au pur hasard. En effet, nous savons qu’il s’agit d’une série aléatoire, vu que c’est ainsi que nous l’avons créée.
Mais comparons tous nos exemples, en appliquant cor.test() à chacune des séries, et en rapportant les résultats dans un tableau. Pour m’éviter cette tâche répétitive, j’utilise la fonction lapply() qui fait précisément cela: elle applique une fonction à tous les éléments d’une liste et qui stocke le résultat dans une nouvelle liste. Je stocke au préalable toutes nos séries dans une liste nommée myseries et je charge les modules magrittr et data.table qui me donnent, respectivement, accès à l’opérateur %>% et à la fonction rbindlist(). Cette dernière me permet de convertir facilement mes résultats stockés sous forme de liste dans un simple tableau. Si vous peinez à comprendre le code qui suit, vous pouvez bien sûr aussi appliquer cor.test() à chacune des séries et rapporter les résultats sur un bout de papier pour les comparer.
library(magrittr)
library(data.table)
myseries <- list(
stationary = y_stationary,
trend = y_trend,
stationary_cyclic = y_stationary_cyclic,
stationary_cyclic_irreg = y_stationary_cyclic_irreg,
trend_cyclic = y_trend_cyclic
)
lapply(seq(myseries), function(i){
ct <- cor.test(t,myseries[[i]])
c(
type = names(myseries)[[i]],
ct$estimate %>% round(3),
p.value = ct$p.value %>% round(3),
conf.int1 = ct$conf.int[1] %>% round(3),
conf.int2 = ct$conf.int[2] %>% round(3)
) %>% unlist %>% t %>% data.frame
}) %>% rbindlist Code language: R (r)J’obtiens le tableau suivant:
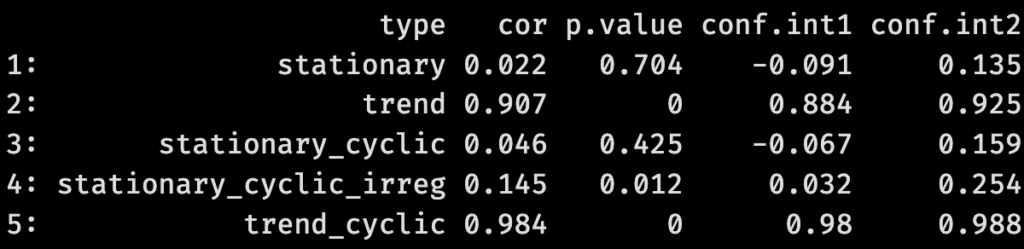
Comme on le voit, nos deux séries non-stationnaires (“trend” et “trend_cyclic”) montrent des corrélations entre valeur et temps nettement plus fortes que dans les autres séries, et surtout plus significatives avec des p-values inférieures à 0.1%. C’est rassurant: nous savons en effet que les valeurs de ces deux séries augmentent avec le temps. Pareillement rassurant: les séries stationnaires 1 et 3 ne passent pas le test; leurs corrélations avec le temps sont faibles (2% et 4% respectivement) et leurs p-values (70.4% et 42.5%) ne permettent pas de rejeter “l’hypothèse nulle” d’une corrélation due au pur hasard. Mais une valeur demeure troublante: celle de notre “série 4” avec son cycle irrégulier. Dans ce cas, l’algorithme détecte une corrélation de 14.5% avec sa p-value de 1.2%, donc significative à p<5% qui est le seuil de tolérance accepté dans la plupart des tests statistiques. Dans de nombreuses études publiées, un tel résultat serait reconnu comme statistiquement validé et l’auteure pourrait conclure à une croissance modérée du phénomène mesuré par les valeurs de la “série 4”. Or, nous savons que la tendance de cette série est stationnaire!
Dans ce sens, un test de corrélation générique offre un outil plutôt valide pour tester la non-stationnarité; il faut néanmoins se méfier des séries à cycle irrégulier. Une différence de fond persiste surtout entre
- d’un côté, la corrélation entre deux variables mesurées sur de nombreux individus à un moment donné – comme le “PIB” et “l’espérance de vie” que l’on mesurerait pour chaque pays du monde en 2023
- et de l’autre, l’autocorrélation d’une seule variable mesurée sur un seul individu à plusieurs moments du temps – comme l’évolution de la température de l’air enregistrée par une station
Une série temporelle renvoie au second cas de figure. À ces différences de fond s’ajoute que le temps n’est pas une variable comme une autre: un lac peut se réchauffer puis refroidir, un humain peut grossir puis maigrir, un PIB peut fluctuer, mais rien ni personne ne peut revenir en arrière dans le temps. Contrairement à l’écrasante majorité des variables mesurées dans les tests de corrélation génériques, l’axe du temps est irréversible. Il est du moins convenu de le considérer comme tel. On peut bien sûr imaginer une ontologie (une théorie philosophique portant sur l’être des choses) où ces différences seraient gommées. Si vous adoptez une posture bouddhiste radicale, la continuité des objets dans le temps n’est qu’illusion (moha, mâyâ): dans ce cadre, mesurer plusieurs fois le même individu ou mesurer plusieurs individus distincts revient au même. Similairement, si vous adoptez la théorie d’un univers-bloc (nommée ainsi par le philosophe Thomas Davidson et associée notamment à la théorie de la relativité restreinte), vous affirmez que le futur existe déjà et que le passé existe encore; la succession des moments du temps étant une illusion; en d’autres mots, vous pensez que le temps est une dimension comme une autre. Mais le pensez-vous vraiment? Si ce n’est pas le cas, utiliser un test de corrélation générique pour vérifier la non-stationnarité d’une série temporelle pourrait vous engager à votre insu dans une position philosophique radicale!
Les mathématiques offrent des tests mieux ciblés comme le test de Ljung-Box ou le test KPSS. Les fonctions de R les rendent accessibles à tou.te.s
Le test de Ljung-Box
Le test de la statisticienne finnoise Greta Ljung (et de son directeur de thèse George Box) examine l’autocorrélation d’une série temporelle. Son “hypothèse nulle” est d’avoir affaire à du “bruit blanc”, un terme inspiré de la musique électronique et dénotant une série temporelle aléatoire. Une série non-stationnaire aura une faible p-value et permettra donc de rejeter l’hypothèse nulle. Essayons avec une série stationnaire
Box.test(y_stationary, lag=25, type="Ljung-Box") Code language: JavaScript (javascript)Nous obtenons ceci:
Box-Ljung test
data: y_stationary
X-squared = 31.067, df = 25, p-value = 0.1868La p-value est élevée (18.7%). Le test ne nous permet donc pas de rejeter l’hypothèse d’avoir affaire à du bruit blanc: une bonne chose, vu qu’il s’agit, en effet, de valeurs aléatoires que nous avons générées autour d’une valeur moyenne. Voyons les résultats du même test pour les autres séries:
lapply(seq(myseries), function(i){
act <- Box.test(myseries[[i]], type="Ljung-Box")
c(
type = names(myseries)[[i]],
p.value = act$p.value %>% round(3)
) %>% t %>% data.frame
}) %>% rbindlistCode language: R (r)Nous obtenons ceci:

La p-value est inférieure à 0.1% pour toutes les autres séries. Un résultat rassurant, vu que, dès qu’il y a évolution progressive ou cycle, la série ne peut en effet plus être considérée comme du bruit blanc. Le test de Ljung-Box le détectera, mais il sera incapable de distinguer entre la cyclicité et la tendance à long terme.
Un autre défaut de ce test est que son résultat dépend fortement du paramètre “lag”. Plus haut, nous avons arbitrairement choisi lag=25. Mais avec un lag=3, Box.test(y_stationary, lag=3, type="Ljung-Box") retourne une p-value de 2.3%, et permet donc d’affirmer qu’il ne s’agit pas de bruit blanc… La littérature regorge de conseils contradictoires quant au choix de la valeur de paramètre “lag” optimal en fonction de la longueur totale de la série temporelle analysée (voir Hassani & Yeganegi 2020 listés en bibliographie à la fin de ce tutoriel). Une approche visuelle facilitera notre jugement:
boxtests <- sapply(seq(myseries), function(i){
sapply(1:30,function(x){
testres <- Box.test(myseries[[i]], lag=x, type="Ljung-Box")
testres$p.value
})
}) %>% as.data.table %>% setNames(names(myseries))
boxtests$lag <- 1:nrow(boxtests)
ggplot(
boxtests %>% melt(id.vars = "lag") %>%
setNames(c("lag","series","p.value"))
) +
geom_bar(
aes(lag,p.value,
fill=ifelse(p.value>0.05,"green","red"),
colour=ifelse(p.value>0.05,"green","red")
),
stat = "identity",
) +
facet_grid(rows="series", space = "free_y") +
guides(fill=guide_legend("hypothèse nulle"), colour = "none") +
scale_fill_discrete(labels=c('rejetée', 'retenue')) +
theme(strip.text.y.right = element_text(angle = 0),legend.position="bottom")Code language: R (r)
Si vous ne comprenez pas le graphique ci-dessus, ne vous inquiétez pas, cela n’a pas d’importance pour la suite de ce tutoriel. Je veux simplement montrer aux spécialement intéressés que, oui, la p-value du test Ljung-Box descend parfois en dessous du seuil de 5% pour certaines valeurs du paramètre “lag” même lorsque l’algorithme examine notre première série stationnaire; mais cette p-value reste systématiquement à zéro pour toutes les autres séries! Aussi bien pour les cycliques que pour les évolutives à long terme. Le test Ljung-Box demeure donc fiable pour détecter la non-stationnarité d’une série temporelle.
Le test Kwiatkowski-Phillips-Schmidt-Shin (KPSS)
Le test KPSS comble plusieurs manques du test de Ljung-Box. Son “hypothèse nulle” est que la série est “niveau-stationnaire” (level-stationary, trend-stationary), en d’autres mots qu’elle n’évolue pas, qu’elle ne possède pas de tendance (trend), même lorsqu’elle est cyclique. La p-value du test KPSS sera donc faible pour les séries qui évoluent sur la durée. Essayons à l’aide de la fonction kpss.test() du module tseries:
library(tseries)
kpss.test(y_stationary,null="Level",lshort=F) Code language: R (r)Nous obtenons:
KPSS Level = 0.13206,
Truncation lag parameter = 15,
p-value = 0.1Cette p-value est relativement faible (10%) mais ne permet tout de même pas d’affirmer que la série ne serait pas stationnaire avec un niveau de significativité habituellement requis (p<5%). Une bonne nouvelle, vu que nous savons qu’elle est bien stationnaire. Comparons les résultats pour toutes les séries
lapply(seq(myseries), function(i){
act <- kpss.test(myseries[[i]],null="Level",lshort=F)
c(
type = names(myseries)[[i]],
p.value = act$p.value %>% round(3)
) %>% t %>% data.frame
}) %>% rbindlistCode language: PHP (php)
Très clairement, les deux séries évolutives (la 2 et la 5) passent le test: avec leur p-values de 1%, nous pouvons sans autres rejeter l’hypothèse nulle de leur stationnarité avec un niveau de significativité standard p<5%. Ceci n’est pas le cas pour les séries que nous savons dépourvues de tendance. Toutes leurs p-values dépassent 10%, y compris celle de la “série 4” stationnaire avec cycle irrégulier que le test de corrélation générique avait “déclarée” non-stationnaire. Le test KPSS s’avère donc bien plus fiable que le test de corrélation générique.
En conclusion, le test KPSS de la tendance, en combinaison avec le test du bruit blanc Ljung-Box donne des résultats plus fiables que le test de corrélation générique. Ils sont aussi plus facilement interprétables sans avoir à passer par des ontologies exotiques comme celle d’un univers-bloc.
Je recommande de faire systématiquement les trois tests et de comparer leurs résultats pour s’assurer de la validité de vos affirmations.
La méta-approche du “modèle linéaire”
Il existe aussi des méta-approches. Plutôt que de conduire des tests directement, de nombreux usagers de R recourent à des fonctions de haut niveau, comme celle qui produit un modèle linéaire – linear model – lm() et de nombreuses métriques associées. Dans sa forme la plus basique, cette modélisation – qui était le nec plus ultra au 19e siècle – consiste à calculer les coefficients a et b pour l’équation:
De vos anciens cours de mathématiques, vous vous rappelez peut-être que a correspond à “l’intercept” où la ligne de régression coupe l’axe des y, et que b correspond à la pente de la ligne. Le modèle linéaire peut être incorporé directement dans un graphique ggplot, pour générer voir la ligne de régression superposée aux données d’origine:
library(ggplot2)
ggplot( cbind(myseries %>% as.data.table,t) %>% melt(id.vars="t") ) +
geom_line(aes(x=t,y=value)) +
stat_smooth(aes(x=t,y=value), method = "lm", col = "red",linewidth=0.5) +
facet_grid(facets="variable") +
theme(strip.text.y.right = element_text(angle = 0),legend.position="bottom")Code language: JavaScript (javascript)
Vous pouvez demander au module de tester le méta-modèle linéaire, ici pour la série 1 (stationary):
lm(formula = y_stationary ~ t) %>% summaryCode language: R (r)Résultat:
Residuals:
Min 1Q Median 3Q Max
-0.243514 -0.042364 -0.003054 0.048293 0.215665
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.978e-01 8.815e-03 56.48 <2e-16 ***
t 1.937e-05 5.102e-05 0.38 0.704
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.07653 on 298 degrees of freedom
Multiple R-squared: 0.0004836, Adjusted R-squared: -0.002871
F-statistic: 0.1442 on 1 and 298 DF, p-value: 0.7044Ce qui nous intéresse d’abord ici est la colonne “estimate” des coefficients. Comme son nome l’indique, il s’agit d’estimateurs des coefficients a et b dans la formule mentionnée y=a+bt. Dans cette présentation du résultat peu conviviale, a est le coefficient de l’Intercept et vaut 0.5; b est le coefficient de t, c’est-à-dire la pente et vaut 0.00002: une pente positive extrêmement faible. Le résultat du test nous dit aussi si cette pente est significative. En l’occurrence, elle ne l’est pas pour la série série 1 (stationary), vu que la p-value, donnée dans la colonne “Pr(>|t|)“, est de 0.704 et ne nous permet donc pas de rejeter l’hypothèse nulle. Mais voyons ce qu’il en est pour les autres séries:
lapply(seq(myseries), function(i){
ctest <- lm(formula = myseries[[i]] ~ t)
ctestsum <- summary(ctest)
data.table(
type = names(myseries)[[i]],
a = ctest$coefficients[1],
a_pvalue = ctestsum$coefficients[1,4],
b = ctest$coefficients[2],
b_pvalue = ctestsum$coefficients[2,4],
r2_glob = ctestsum$r.squared,
r2adj_glob = ctestsum$adj.r.squared
) %>% data.frame
}) %>% rbindlistCode language: R (r)
Après un examen attentif de ces tests, on remarque que la série “stationary_cyclic” possède tout de même une pente sur le long terme faible, 0.001, mais quasiment significative, avec une p-value (b_pvalue) de 4.3%. Or, nous savons que cette série est cyclique mais sinon totalement stationnaire. Une nouvelle fois, si nous avions affaire à des données empiriques, il vaudrait la peine de conduire un test KPSS pour vérifier s’il est lieu d’exclure une lente croissance de nos valeurs.
Analyse de points d’inflexion
Pour comprendre l’analyse de points d’inflexion, créons d’abord une série temporelle fictive dont la structure change en cours de route:
set.seed(100)
y_changes <- c(
rnorm(80, 0, 1),
rnorm(40, 1.5, 2),
rnorm(70, 0, 1),
rnorm(110, -0.8, 0.5)
)Code language: R (r)La fonction rnorm(i, m, s) génère i valeurs autour de la moyenne m et avec l’écart-type s. Nous produisons donc une série qui commence par 80 nombres autour de la moyenne 0, puis 40 nombres autour de la moyenne 1.5, puis 70 nombres autour de la moyenne 0, enfin 110 nombres autour de la moyenne -0.8. Nous varions aussi d’écart-type pour chaque partie de la séquence. Jetons un coup d’oeil à la série générée:
plot(y_changes, type="l")
abline(v=c(80,120,190),col="green",lwd=2)Code language: JavaScript (javascript)
Le défi de l’algorithme sera de retrouver ces segments – que nous, créateurs de la série, sommes les seuls à connaître – en identifiant les points d’inflexion aux instants 80, 120 et 190 de la série. Plusieurs modules de R proposent cette fonctionnalité, dont bcp, et changepoint et strucchange. Ce dernier est le plus abouti.
Le module strucchange
Le module strucchange exige de travailler explicitement avec une série temporelle, ce qui, en R, se traduit par un “objet” de type ts. Si vous ne comprenez pas ce que cela veut dire, sachez simplement qu’il faut convertir le vecteur y_changes qui représente votre série temporelle à l’aide de la fonction as.ts. Cette conversion est facile
library(strucchange)
y_changes.ts <- as.ts(y_changes)Code language: R (r)Détectons maintenant les points d’inflexion à l’aide de la fonction strucchange::breakpoints(). La fonction demande une “formule”, dont la variante visant à détecter les changements de moyenne, qui convient à notre cas, est y_changes.ts ~ 1 . En générant le graphisme du résultat, nous pouvons demander de voir aussi les intervalles de confiance de points d’inflexion.
sc_bp <- breakpoints(y_changes.ts ~ 1)
plot(y_changes.ts)
lines(fitted(sc_bp),col="red",lwd=3)
lines(confint(sc_bp),lwd=2,col="blue"Code language: R (r)
Comme on le constate, strucchange::breakpoints() détecte très justement les points d’inflexion dont nous avons volontairement doté notre série. Cette fonction peut en outre détecter les changements de tendance. Pour tester, reprenons notre série 2 (y_trend). Pour rappel, nous avons généré cette série en cumulant des valeurs aléatoires autour d’une moyenne de 1 et avec un écart-type très large de 6, puis nous l’avons “normaliée” en faisant en sorte que toutes ses valeurs soient comprises ent 0 et 1.
y_trend <- cumsum(rnorm(length(t),mean=1,sd=6))
y_trend <- y_trend/max(y_trend)Convertissons-la en série temporelle et analysons si sa tendance possède des points d’inflexion. La formule appropriée pour la fonction breakpoints pour ce cas de figure est y_trend.ts ~ t, où t représente le temps (un simple vecteur de chiffres allant de 0 à 299 que nous avons défini au début de ce tutoriel):
y_trend.ts <- as.ts(y_trend)
sc_tc <- breakpoints(y_trend.ts ~ t)
plot(y_trend.ts)
lines(fitted(sc_tc),col="red",lwd=3)
lines(confint(sc_tc),lwd=2,col="blue")Code language: R (r)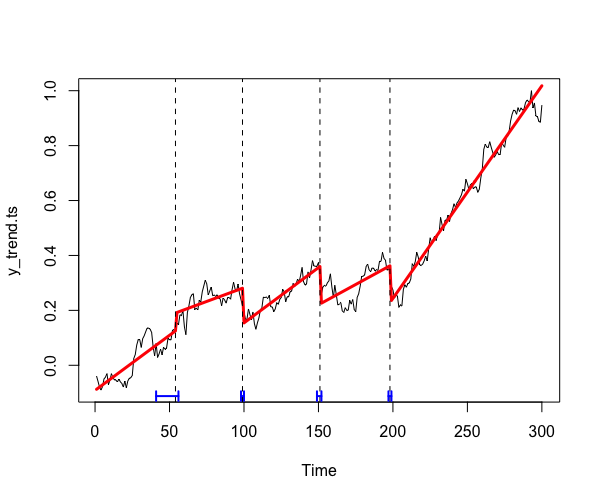
Nous constatons que l’algorithme détecte des changements dans la tendance de cette série temporelle pourtant purement aléatoire. Avouons tout de même qu’à l’œil nu, son analyse semble crédible. Cela nous rappelle que des structures peuvent apparaître même là où aucun phénomène sous-jacent n’est en jeu. Les algorithmes peuvent parfois vous aider à déjouer vos projections mais, comme l’illustre le présent exemple, ils peuvent aussi les confirmer. Même hybridé à l’algorithme, l’esprit humain demeure infiniment capable d’halluciner un sens du réel, ce qui fait sans doute le charme de nous tou.te.s et le fondement de nos cultures.
Des moyens d’analyse plus avancés de points d’inflexion de séries temporelles sont expliqués dans la documentation du module strucchange.
Analyse des cycles
Pour l’exemple, définissons d’abord quelques cycles parfaitement réguliers.
k <- 2*pi / (max(t)/2) # ceci pour s'assurer qu'il y a 2 cycles entier sur la durée du temps t
tonic <- sin(k * t)
third <- sin(k * 3*t) / 3
fith <- sin(k * 5*t) / 5
seventh <- sin(k * 7*t) / 7
ggplot() +
geom_line(aes( x=t, y=tonic )) +
geom_line(aes( x=t, y=third ), color="green", alpha=0.6) +
geom_line(aes( x=t, y=fith ), color="blue", alpha=0.6) +
geom_line(aes( x=t, y=seventh ), color="red", alpha=0.6) +
geom_vline(xintercept = c(50,100,150,200,250), linetype="dashed",color="green") +
geom_vline(xintercept = c(150), linetype="dotted") +
ylab("amplitude")Code language: PHP (php)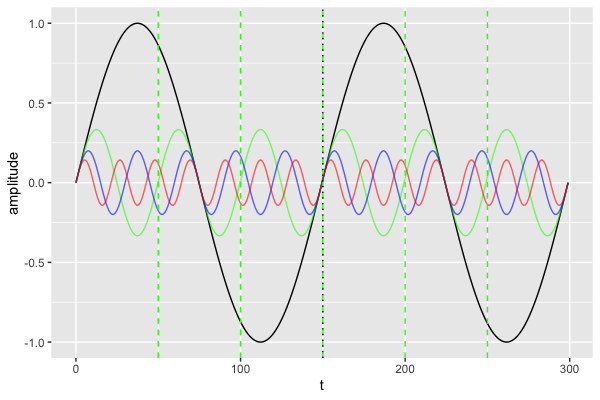
Nous avons:
- 2 cycles complets de la série noire,
- 6 cyles de la série verte,
- 10 cycles de la bleur, et
- 14 cycles de la rouge.
Retenons ces fréquences car nous les reverrons à la fin de l’analyse. Notez que ces fréquences sont relatives à la totalité de la durée de notre série (300) et qu’elles pourraient aussi être exprimées comme 2/300 (=0.006), 6/300 (=0.02) etc. Pour nos facilier la vie, toutefois, nous allons cosidérer que l’ensemble de notre série représente notre unité de temps. Si vous faites de la musique, vous remarquerez que les rapports de longueur entre ces cycles (1, 3, 5 et 7) correspondent aux rapports des fréquences entra la tonique, la tierce, la quinte et la septième. Si vous les jouez simultanément, vous entendrez un accord de septième. Mathématiquement, “jouer simultanément” quatre fréquences revient à les superposer, et se traduit par une addition:
y_harmonic <- tonic + third + fith + seventh
ggplot() + geom_line(aes(t,y_harmonic))
L’analyse de Fourier
Imaginez maintenant que vous voyez la série temporelle ci-dessus, et que l’on vous demande de retrouver les fréquences de base des cycles additionnés dont elle résulte (et que vous ne connaitriez pas). La tâche est autrement plus difficile que l’addition que nous venons de faire. C’est là qu’interviennent les transformées de Joseph Fourier, un mathématicien qui a montré que tout cycle périodique peut être représenté par une somme de cycles sinusoïdaux simples. Nous appelons aujourd’hui une telle somme “série de Fourier”. Pour détecter les cycles de base dans une série temporelle, nous pouvons nous servir d’une transformée de Fourier. Ne prenez pas peur en voyant des formules dans cette section du tutoriel, il n’est pas nécessaire de les déchiffrer pour comprendre le résultat d’une analyse de Fourier. L’essentiel est de savoir produire un périodogramme et l’interpréter ainsi que nous le ferons à la fin.

Voici d’abord la formule d’une transformée de Fourier vérifiant l’intensité de la présence d’une fréquence donnée f dans une série cyclique y de longueur totale tn (i dans cette formule sert de séprateur entre la part réelle et la part imaginaire du nombre complexe πift; e est la constante de Néper et d nous indique que l’on différencie sur t) :
L’astuce d’une analyse de Fourier consiste à appliquer cette transformée à la série originelle y, en passant en revue toutes les fréquences possibles f variant entre 0 et la longueur totale de y (300). L’algorithme Fast Fourier Transform, incarné par la fonction fft() de R, permet d’accomplir cette tâche à peu de frais:
freqspec <- fft(y_harmonic)Son résultat est une suite de nombres complexes de type a+ib, comportant une composante réelle (a) et imaginaire (b). Nous pouvons visualiser séparément la partie imaginaire et la partie réelle:
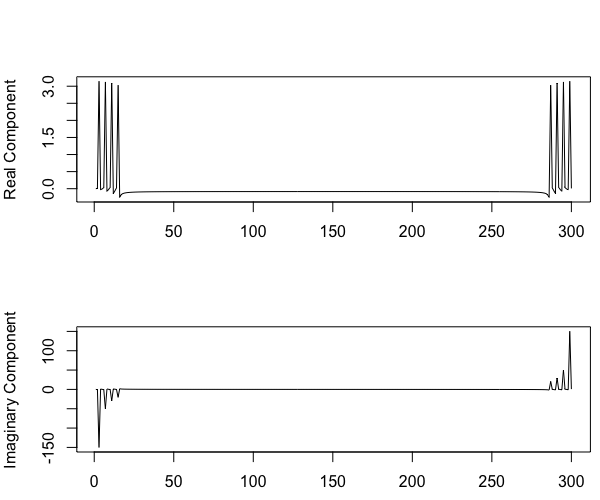
Comme vous le pensez sûrement, de tels nombres sont difficiles à interpréter, mais on peut calculer la “valeur absolue” – aussi appelée module – de cette nouvelle série en appliquant à chacun de ses nombres la formule qui suit:
Dans R, cela peut se faire à l’aide de la fonction abs() ou de la fonction Mod(), strictement équivalentes. Nous arrivons alors presque au bout de l’analyse, car visualiser la valeur absolue d’une transformée de Fourier d’une série temporelle revient à construire un “périodogramme” de cette série:
freqspec.abs <- abs(freqspec)
plot(freqspec.abs,type="l",xlab="Frequency", ylab="Strength")Code language: HTML, XML (xml)
Les sommets de ce périodogramme vous révèlent les fréquences de base dont l’addition a généré la série. Vous aurez noté que ce diagramme est symétrique. Ceci est dû à un artefact d’échantiollonnage de l’algorithme de FFT expliqué ici. Nous pouvons ignorer le côté droit de la symétrie et ne conserver que la partie gauche:
freqspec.abs.sel <- freqspec.abs[1:(length(freqspec.abs)/2+1)]Code language: R (r)Vous pouvez récupérer les valeurs et les positions exactes des sommets en utilisant par exemple le module pracma:
library(pracma)
peaks <- findpeaks(freqspec.abs.sel)
peaksCode language: R (r)Résultat:
[,1] [,2] [,3] [,4]
[1,] 149.92479 3 1 5
[2,] 49.76625 7 5 9
[3,] 29.57524 11 9 14
[4,] 20.69745 15 14 151Code language: JSON / JSON with Comments (json)La première colonne de cette matrice vous donne les valeur d’amplitude (strength), la seconde colonne expose les fréquences que nous cherchons, pour peu d’en soustraire 1.
frequencies <- peaks - 1Code language: R (r)Résultat:

Nous retrouvons très exactement les fréquences totales des cycles que nous avons crée à l’origine! Nous retrouvons même, presque exactement, les rapports entre les amplitudes:
amplitudes.relative <- max(peaks[,1]) / peaks[,1] Code language: R (r)
Il n’est pas nécessaire de comprendre exactement pourquoi cela marche pour exploiter le potentiel de cette approche, mais cette excellente vidéo peut vous y aider:
Pour tout scintifique, ce méthode d’avère utilie pour isoler des phénoènes caclique qui se superposent dans l’ampleur d’un phénomèe et constitue souvvent le pas pour en comprendre les causes.
Les spectrogrammes
(cette partie est en cours d’élaboration, patience)
Les séries cycliques et saisonnières
L’analyse de séries temporelles porte l’héritage de l’économétrie. Cette discipline avide de prédictions – notamment au sujet de valeurs boursières – a bien contribué aux méthodes d’analyse temporelle, mais leur a aussi imprimé son vocabulaire et sa manière de penser. Par exemple, les économètres parlent parfois de phénomènes “cycliques” ou “saisonniers”; parmi eux, certains essaieront de vous expliquer la différence entre ces deux types de récurrences en disant que les séries cycliques sont irrégulières, tandis que les séries saisonnières seraient régulières, car liées à des durées fixes (cycles hebdomadaires, mensuels, annuels…). Nous rencontrons là les limites du boursicoteur qui s’imagine multiplier à l’infini son capital dans un univers immuable: ses lundis, ses weekends, les repas de midi, les Noëls, le budget de fin d’année…; les révolutions ou les catastrophes naturelles le prennent toujours au dépourvu et il essaiera soit de les empêcher, soit d’en nier l’existence. En effet, distinguer la cyclicité de la saisonnalité est dépourvu de sens mathématique, et atteste simplement d’une faible capacité d’abstraction, étant donné que les saisons sont elles aussi des cycles, liés à des phénomènes physiques et sociaux relativement complexes: le mouvement de la terre et de la lune autour de leurs orbites respectives, ainsi que les diverses récurrences de pratiques sociales organisées autour du calendrier grégorien et du septénaire mésopotamien. Pour distinguer les degrés de complexité des cycles, parlons donc plutôt de cycles “réguliers”, “complexes”, ou “chaotiques”.
Le seul intérêt à distinguer cycle et saison en économie émane du fait que les comportements humains liés au calendrier et aux heures du jour relèvent de conventions connues et sont donc prévisibles et faciles à expliquer, tandis que les logiques des cycles d’expansion et de dépression économiques suivent des logiques endogènes qui échappent en grande partie au contrôle social. Pour mieux les comprendre, il est utile de les isoler au sein des variations saisonnières, par exemple à l’aide des modules R forecast ou bfast. Seul l’économètre qui vous expliquera la différence entre “cycle économique” et “cycle saisonnier” en ces termes est une économètre crédible.
Solutions
- Exemples concrets pour les figures, la série stationnaire pourrait être l’enregistrement d’un sismographe. La série évolutive: le réchauffement climatique. Série non-stationnaire cyclique: la température enregistrée pendant une semaine au mois de mai.
Ressources supplémentaires
Bai, Jushan, and Pierre Perron. 2003. “Computation and Analysis of Multiple Structural Change Models.” Journal of Applied Econometrics 18 (1): 1–22.
Box, G. E. P. and Pierce, D. A. (1970), “Distribution of residual correlations in autoregressive-integrated moving average time series models.” Journal of the American Statistical Association, 65, 1509–1526. doi:10.2307/2284333.
Bush, E. R., Abernethy, K. A., Jeffery, K., Tutin, C., White, L., Dimoto, E., Dikangadissi, J.-T., Jump, A. S., & Bunnefeld, N. (2017). Fourier analysis to detect phenological cycles using long-term tropical field data and simulations. Methods in Ecology and Evolution, 8(5), 530‑540. https://doi.org/10.1111/2041-210X.12704
Cromwell J. B., W. C. Labys and M. Terraza (1994): Univariate Tests for Time Series Models, Sage, Thousand Oaks, CA, pages 32–36.
Danioko, S., Zheng, J., Anderson, K., Barrett, A., & Rakovski, C. S. (2022). “A Novel Correction for the Adjusted Box-Pierce Test.” Frontiers in Applied Mathematics and Statistics, 8. https://www.frontiersin.org/articles/10.3389/fams.2022.873746
DOLBEAULT Joël, “Einstein et l’univers-bloc”, Revue d’histoire des sciences, 2018/1 (Tome 71), p. 79-109. DOI : 10.3917/rhs.711.0079. URL : https://www.cairn.info/revue-d-histoire-des-sciences-2018-1-page-79.htm
Harvey, A. C. (1993) Time Series Models. 2nd Edition, Harvester Wheatsheaf, NY, pp. 44, 45.
Hassani, H., & Yeganegi, M. R. (2020). “Selecting optimal lag order in Ljung–Box test.” Physica A: Statistical Mechanics and Its Applications, 541, 123700. https://doi.org/10.1016/j.physa.2019.123700
Ljung, G. M. and Box, G. E. P. (1978), On a measure of lack of fit in time series models. Biometrika, 65, 297–303. doi:10.2307/2335207.
Web:
- https://towardsdatascience.com/a-basic-guide-into-time-series-analysis-2ad1979c7438
- https://rpubs.com/richkt/269797
- https://cran.r-project.org/web/packages/testcorr/
- https://cran.r-project.org/web/packages/urca/
- https://cran.r-project.org/web/packages/IrregLong/vignettes/Irreglong-vignette.html
- https://fr.wikipedia.org/wiki/Autocorr%C3%A9lation
- https://rpubs.com/EValenzuela/251324
- https://rpubs.com/euler-tech/stationary_test
- https://cran.r-project.org/web/packages/strucchange/
- https://www.marinedatascience.co/blog/2019/09/28/comparison-of-change-point-detection-methods/
- https://www.r-bloggers.com/2014/11/evaluating-breakoutdetection/
- https://www.youtube.com/watch?v=spUNpyF58BY


