Methods and tools
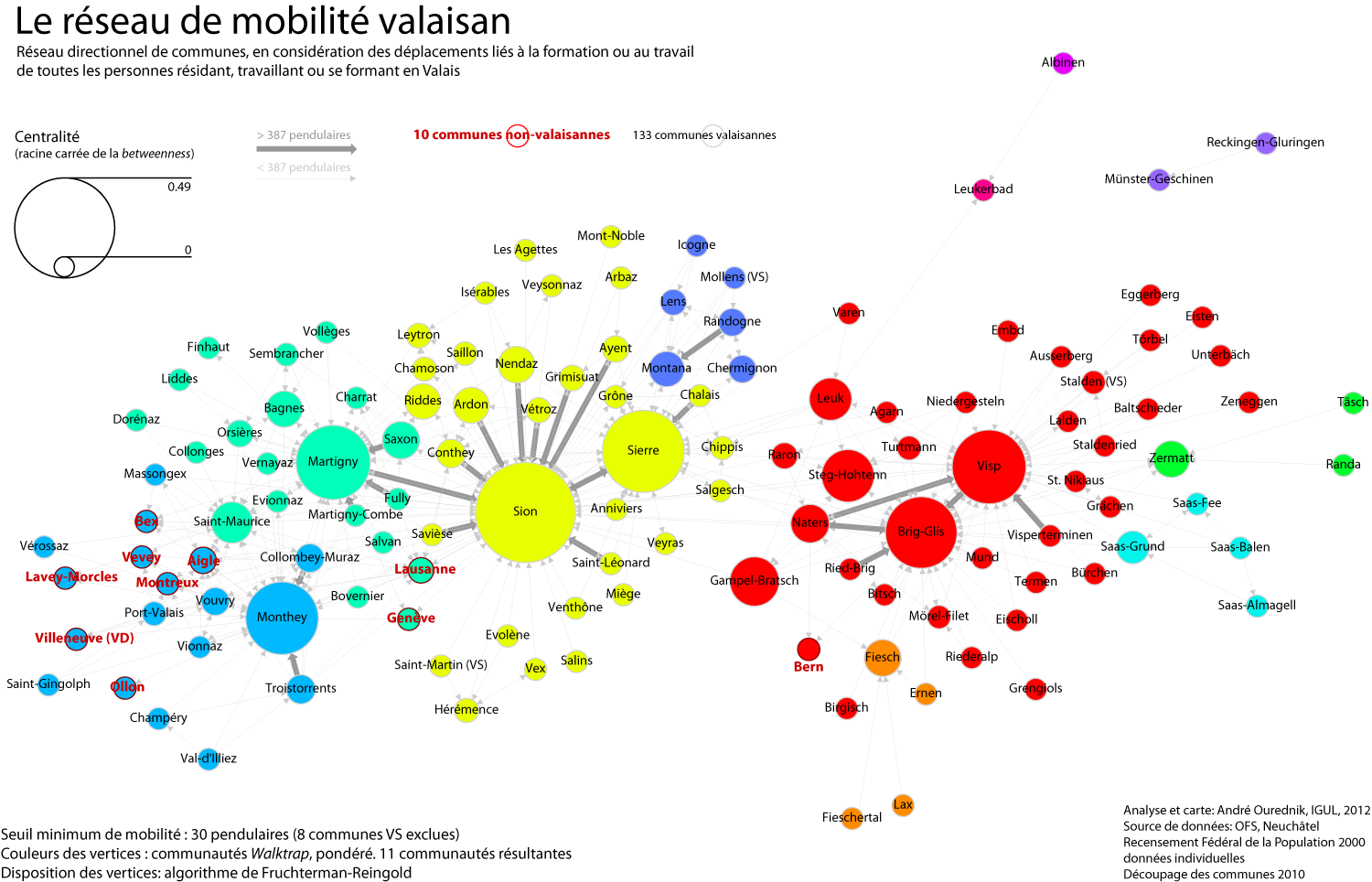
After a day and a half of work and fine-tuning, here we go: the commuting network of all individuals either residing, working or studying in the canton Valais. I’ve used R, with the RStudio GUI, and the igraph library for R. My staring point was the mobility matrix between all communes, including communes outside of the canton, which I’ve calculated from the individual data of the Swiss Federal Census 2000.
I’ve converted my commuting matrix into a directional weighted graph with the graph.adjacency function. I’ve simplified the graph by removing loops.
The vertex size has been determined by betweenness. To reduce size difference, I’ve squared it.
The graphic layout has been obtained with Fruchterman-Reingold algorithm, included in the igraph library.
To determine communities – identified by 11 different colors in the map above – I’ve tried out edge betwenness, leading eigenvector and finally settled for the walktrap community, which gave the most interesting results. Walktrap community, however, remains non-directional. I am still looking for a directional weighted algorithm appropriate for my study case.
The width of the edges depends on the original weights. In other words, thick lines identify paths taken by most individuals.
Some interpretations
As often when reconstructing a network space from a geographical commuting matrix, the resulting space reproduces very closely the topology of the topographic layout of the canton. This is especially understandable in the case of Valais, because of its West to East tree-like structure.
A clear boundary appears between the French-speaking (Monthey, Martigny, Sion, Sierre, Montana) and the German-speaking (Brig-Glis, Visp, Zermatt, Fiesh etc.) communes. Obviously, the linguistic communities exchange only few commuters.
Also interestingly, commuters from Geneva and Lausanne do not connect to the Monthey subnetwork (which would be the closest from these cities further West on the Lac Léman), but share community with Martigny. My earlier unweighted tests with the walktrap algorithm even attached them to Sion. This confirms the hypothesis that larger cities preferentially “interact” with other urban centers, in terms of all types of geographical interaction (commuting, information, financial flows etc.). Smaller cities, like Vevey, Aigle or Montreux, on the other hand, participate preferentially to the Monthey commuting community. Besides their small size, their topographic closeness to the Valais also leads to this.
References
Pons Pascal, Latapy Matthieu (2005), “Computing communities in large networks using random walks” in arXiv:physics/0512106v1 [physics.soc-ph].