Mécanismes rétroactifs de ségrégation, entre une société urbaine et son espace

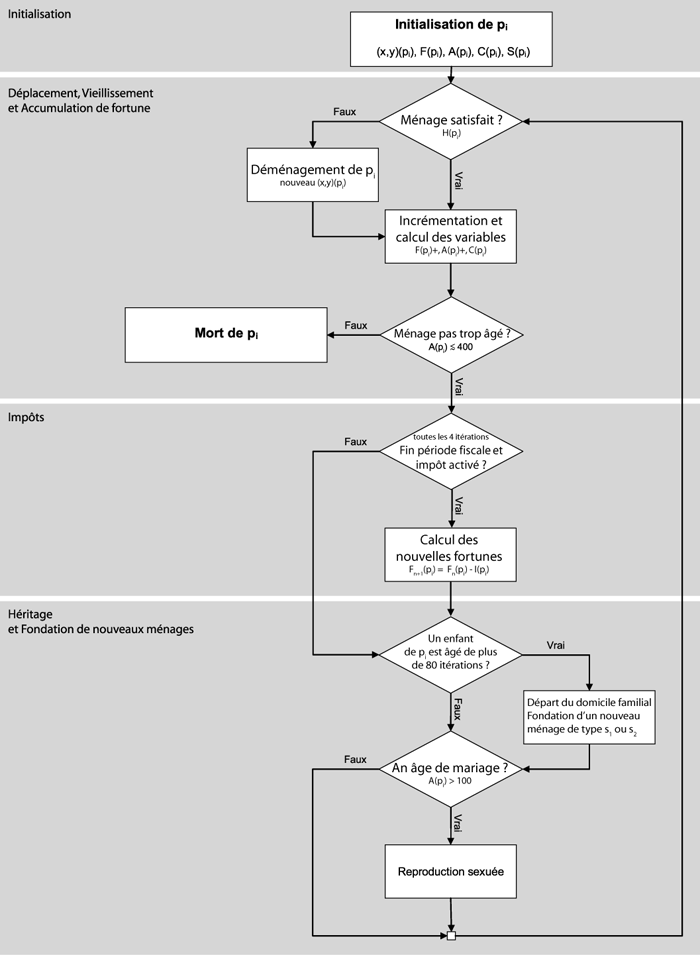
Ceci est un modèle basé agents. Il montre comment la concurrence fiscale entre les communes enrichit les riches et apauvrit les pauvres.

Comment ça marche?

Le modèle combine la 'ségrégation de Schelling' avec un mécanisme d'héritage. Les enfants de familles nombreuses héritent d'un patrimoine divisé (en termes démographiques: le taux de fécondité d'un ménage péjore le statut économique de ses membres).
Au départ, tous les agents disposent des mêmes ressources et sont répartis dans l'espace de manière homogène. Puis un fossé économique s'installe dans la population, suivi d'une ségrégation spatiale.
Les impôts prélevés par zones renforcent la tendance. Ils deviennent moins élevés dans les zones concentrant une population plus riche.

D'OÙ VIENT CE MODÈLE ?

Présenté à ThéoQuant 2005, NOUVELLES APPROCHES EN GEOGRAPHIE THEORIQUE ET QUANTITATIVE, Université de Fanche-Comté et de Bourgogne, Besançon.

Publié dans la Revue Internationale de Géomatique, Dynamiques urbaines et mobilités, vol. 17 no.2/2007, pp. 183-206.

ELEMENTS DU MODELE :

• un espace euclidien de lieux (x, y) représentant un espace urbain.
• quatre quartiers, Q = {q₂₁,q₁₁, q₂₂, q₁₂}.
• une population de ménages, P={p₁,p₂,...,p_n} . Le nombre initial de ménages est paramétrable avec "PCTCOVER"
• un voisinage, V(p_i) ⊂ P, de forme identique pour tout p (toujours un voisinage de Moore de niveau 1).
• un âge, A(p_i) ⊂ [0, 400].
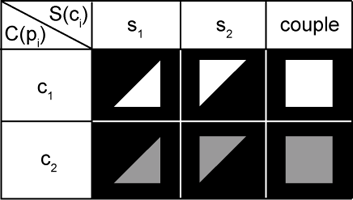
• un "seuil de classe", K, défini par l'utilisateur en termes de % de la fortune médiane. Défini par le paramètre "SEUIL DE CLASSE PCT"
• une classe sociale  (en fonction de la fortune et du seuil de classe):

  C(p) =

  {

  c1⇔F(p) > K c2⇔F(p) < K

• un seuil de tolérance T(c_i), représentant, en %, un taux d'exposition X(p_i) suffisant à motiver le déménagement d'un individu d'un classe c_i. Défini par les paramètres "SEUIL DE TOLERANCE 1" (pour c₁) et "SEUIL DE TOLERANCE 2" (pour c₂)
• un taux d'exposition X(p_i), défini par le nombre des voisins de classe sociale différente relatif au nombre total de voisins; formellement:
  
  

  X(pi ) =

  | { p :( p ∈ V(pi ) ) ∧( C(p) ≠ C(pi ) ) } | | { p : p ∈ V(pi ) } |

• un taux de satisfaction H(p_i), dépendant de l'exposition: H(p_i)≡( X(p_i) < T(c_i) ) . Les ménages insatisfaits déménagent.
• des impôts, I(p_i), calculés séparément pour chaque quartier en fonction des populations |P_Q| et non pas en fonction de la somme des fortunes du quartier ΣF(p_i ∈ P_Q) (en se basant donc sur le principe que tout individu consomme une part égale des ressources publiques). Ceci présente un avantage fiscal pour les quartiers à haute concentration de revenus élevés. Formellement :
  

  	I(pi)	=	F(pi)	(	Σ{p: Q(p) = Q(pi)}	I( Q(pi ) ) F(p)	)
  		où	I( Q(pi ) ) = I(Ω) | {p:Q(p) = Q(pi )} | | P |
  		où	I(Ω) = 0.1 ΣF(p)

Dynamique du système:

Résultats:

1^e simulation — En l'absence d'un mécanisme d'impôts, avec T(c₁) = 40%, T(c₂) = 70% et K = 110% :

2^e simulation — En l'absence d'un mécanisme d'impôts, avec T(c₁) = 40%, T(c₂) = 70% et K = 110% – soit avec des paramètres initiaux identiques à ceux de la 1ère simulation :

3^e simulation — Avec le mécanisme d'impôts actif. Les autres paramètres sont identiques à ceux des simulations précédentes (T(c₁) = 40%, T(c₂) = 70% et K = 110%). Une forte inégalité des quartiers par rapport à leurs taux d'imposition a été enregistrée pour cette dernière : I(q₁₁) = 6.9%, I(q₁₂) = 12.2%, I(q₂₁) = 7.3% , I(q₂₂) = 12.3% 

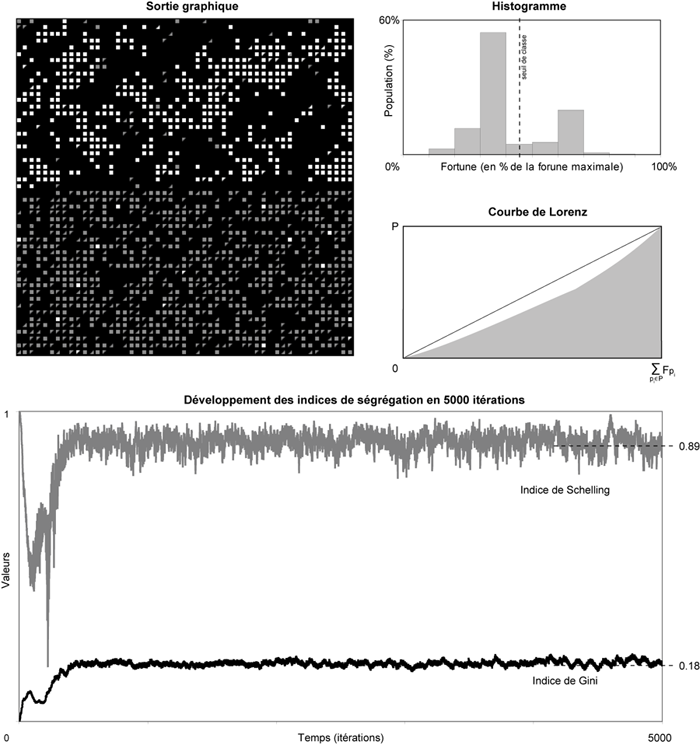
4^e simulation — Avec les paramètres identiques à celle de la figure précédente [3e sim.]. Nous voyons que la concentration de la population « riche » ne s'est développée, ici, que dans le seul quartier q₁₁. I(q₁₁) = 5.9%, I(q₁₂) = 11.9%, I(q₂₁) = 11.9%, I(q₂₂) = 11.3% :

NOTES CONCERNANT LE PROGRAMME :

Le présent applet est un modèle basé agents, qui modélise la dynamique de ségrégation socio-spatiale, résultat d'une synthèse du « modèle de ségrégation de Schelling », du « SugarScape » d'Epstein/Axtel et d'un modèle démographique de dépendance entre les taux de fécondité des ménages et les statuts socio-économiques de leurs successeurs. Le modèle résultant permet de simuler une façon dont un pattern de ségrégation émerge d'une population de ménages initialement aussi bien spatialement que socialement homogène. Le modèle incorpore, d'autre part, une forme de rétroaction de la ségrégation spatiale sur la polarité sociale, incarnée par une mécanisme spatialement inhomogène d'imposition sur la fortune.

Bibliographie

• ANTONI J.-P., Modélisation de l’étalement urbain : une approche méthodologique, Cybergeo, 2002.
• BENENSON I., TORRENS M. P., Geosimulation : Automata-based modeling of urban phenomena, John Wiley and Sons, 2004.
• BIDOU-ZACHARIASEN C., « Gentrification : le tabou français. », Esprit, vol. 3-4, 2004, p. 62-64.
• DAUPHINÉ A., Les théories de la complexité chez les géographes, Anthropos, 2003.
• DELAHAYE J.-P., « La ségrégation urbaine : une fatalité ? », Pour la science, vol. 339, 2006, p. 90-95.
• DONZELOT J., « La ville à trois vitesses : relégation périurbanisation, gentrification », Esprit, vol. 3-4, 2004, p. 14-39.
• DUMONT A., Dépopulation et civilisation : étude démographique, Paris, 1890.
• ENGELEN G.,WHITE R., ULJEE I., « Integrating constrained cellular automata models, GIS and decision support tools for urban planning and policy making », Timmermans H. P. J. (dir.) Decision Support Systems in Urban Planning, , 2002, p. 125-155.
• EPSTEIN J., AXTEL R., Growing Artificial Societies : Social Science from the Bottom Up, Brookings Institution Press., Washington, D.C., 1996.
• OUREDNIK A., La géographie cellulaire. Esquisse d'une épistémologie géographique des automates cellulaires, 2005.
• OUREDNIK A., La philosophie des automates cellulaires, 2004.
• OUREDNIK A., Ségrégation Spatiale des Étrangers en Suisse : D’après les données OFS du recensement de la population 1990, 2004.
• PANCS R., N. V., « Schellig’s spatial proximity model of segregation revisited», Computing in Economics and Finances, 2003.
• PETERSEN W., Population, 3 édition, 1975.
• PRETECEILLE E., Ségrégations Urbaines, L’Harmattan, Paris, 1995.
• SCHELLING T. C., « Dynamic Models of Segregation », Journal of mathematical sociology, vol. 1, 1971, pp. 143-186.
• SCHELLING T. C., Micromotives and Macrobehavior, Norton, New York, 1978.
• SOJA E. W., « Writing the city spatially », City, vol. 7, 2003, p. 270-280.
• WILENSKY U., NetLogo, Center for Connected Learning and Computer-Based Modelling. Northwestern University, Evanston, IL, 1999.