What we call Artificial Intelligence reflects a thousand-year-old aspiration to provide thought with rules. It was born with the first cities, whose walls, selective doors, stairs, and secret passages gave new directions and meaning to human mobility. Four thousand years ago, a Sumerian scribe engraves King Ur-Nammu’s code on a clay tablet with a stylus and then leaves it out in the sun. The artifact hardens and fixates the laws of the city of Ur. Its code replaces the spontaneous intelligence of a judge, subject to the arbitrariness of cruelty or clemency. It has a casuistic form: if a man is accused of witchcraft, then he must undergo the test of cold water; if his innocence is proven, then his accuser must pay 3 shekels, etc.
From program to reasoning
The law is a program executed by a society’s judiciary system. Its mode of thought is dogmatic because it is limited to imposing precepts without proving their correctness. Like the ātmavidyā, that merely asserts dogmas about the soul. Unlike the science of reasoning ānvīkṣikī (~650 BC) that seeks to demonstrate them. The latter includes hetu-śāstra, the theory of reason, which the venerable Medhātiti Gautama (~550 BC) develops into a “science of right and true reasoning”. The logic Nyāya-śāstra, thus founded at the foot of the Himalayas, defines among other things pratyakṣa, the science of perception, anumāṇa, the rules of inference and upamāṇa, the rules of comparison (Vidyabhusana, 1920).
One hundred years later, the sophist Protagoras distinguished the modalities of speech between questions, answers, prayers, and injunctions. As in India, the rules of Greek logic are articulated with those of the grammar imposed by the written word. The historian Callisthenes accompanies Alexander in his Asian campaigns and perhaps brings texts from Nyāya-śāstra to his nephew Aristotle (384-322 BC) who elaborates the idea of the syllogism (Kak, 2005). Translated into Syriac and then into Arabic, Aristotle’s writings returned to Christian Europe under the name of Imam Arastu. Muḥammad al-Khwārizmī (780-850) founded the arithmetics of numerical reasoning and bequeathed to modern languages two words derived from the Latin form of his own name, Algoritmi: algebra and algorithm. In the 13th century, Ramon Llull, a Catalan, soldier, priest, missionary, mystical writer, proposed a language of symbols to express Syllogisms, to which George Boole (1815-1864) gave his first modern form in his algebra: if A is true and B is false, is it true to say that A or B is true? A=1, B=0, ⊨ A∨B? The question of truth obsesses logic. Boole gives the value 1 to the truth, which also denotes the universe. 0 is devoted to the false, which is nothing. 1-A is the complement of A: the universe without A. In the eyes of logic, we live in the complementary universe of everything that is no longer or has never been.
Mechanization of thought

The symbolization of thought opens the way to its mechanization, which consists in translating its presumed rules into the workings of machines and then into their electrical circuits. Divine statues in Hellenic Egypt (~200 BC) moved, professed and inspired faith, moved by hydraulic power and the hidden hands of priests. Tibetan prayer wheels recite mantras. But the real metamorphosis of symbols into mechanical movements takes the form of rigid pieces of paper with perforations. The presence or absence of a perforation in a given position is interpreted by the steel fingers of a machine. Such punched cards, conceptually very similar to DVDs and Blue Ray, are first used in looms and barrel organs. In the 18th century, artificial intelligence was at the service of aesthetic experience, which culminates for instance in the sophistication of the anthropomorphic automatons of the Jacquet-Droz.
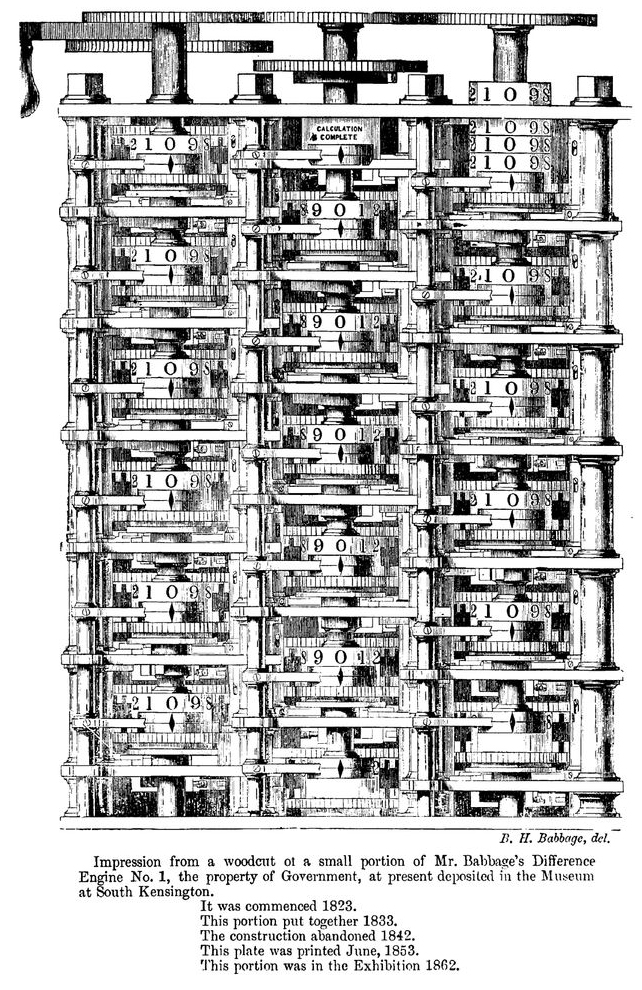
At the beginning of the 19th century, Charles Babbage imagined the analytical machine: a device the size of a cabinet capable of solving problems submitted via perforated cards. A control unit manages the order of the symbols for processing by a mill that transfers them to a mechanical printer.
Ada King, Countess of Lovelace, daughter of the poet Byron, met Babbage at the age of 17. Ten years later, she wrote the first algorithm for her machine; today, many considered it to be the ancestor of all programs. It would be 120 years before a German engineer wrote the word Informatik for the first time. Ada Lovelace thought that “the Machine could compose scientifically and elaborately pieces of music of any length or degree of complexity”.
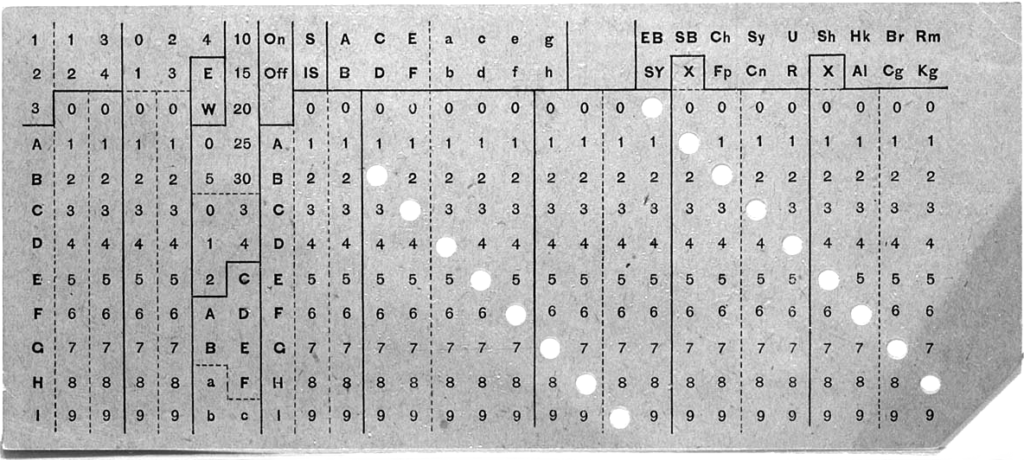
But just like writing, born of the desire to impose rules on reality hundreds of years before any attempt at literature, the mechanical thinking of the late 19th century was first tackled by the bureaucracy. Hermann Hollerith integrates the punched cards into a device bearing his name and adopted by the U.S. Census Bureau. He eventually leaves the administration to found what would later become the International Business Machines Corporation, IBM. The Arbeiter-Unfall-Versicherungs-Anstalt für das Königreich Böhmen acquires the machine; this is how project manager Franz Kafka discovers it. In 1919, it
Codes of ethics
Since our origins, contradictory ethical codes have clashed through speech and writing. In the 20th century, the field of struggle expands into computer science. In 1936, Alan Turing conceptualized computer calculation according to a model that is still in use today. From the beginning of the Second World War, he led a group of cryptologists who increased the computing power of the Polish electromechanical device Bomba kryptologiczna by a factor of 100 to crack the Nazi transmission code generated by the Enigma machine. They succeeded in doing so as early as 1940 and shortened the duration of the war by two years.
In 1950, Turing also defined a test to evaluate the ability of a thinking machine, which science fiction would call the Turing test (Clarke, 1968, Chapter 16). A human is talking with a computer and another human hidden behind a curtain. If the person is unable to say which of his or her interlocutors is a computer, the computer is considered to be thinking. The test is based on an evening game where a man and a woman, also hidden, try to make the public believe that they are both women or both men through written messages.
Two years later, Turing was sentenced to chemical castration by a British court because of his homosexuality and committed suicide by eating an apple injected with cyanide.
The unlikely emergence of scientific fields
The term artificial intelligence appeared in the same decade. In 1956, a Dartmouth professor used it in a funding application for a two-month workshop with about ten mathematicians. The choice of the term allows him to avoid “cybernetics” and the presence of its pundits. This is how artificial intelligence becomes a research field in its own right. Its broadest field today is machine learning.
Through machine learning, a program “evolves”: it increasingly recognizes forms by training its neuromimetic network, a much simpler construction than its name suggests.
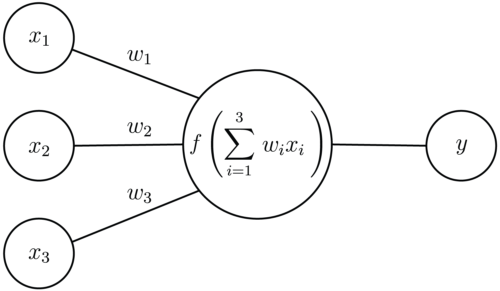
Such a network begins with several inputs – say x1 to x3 – comparable to the cells of the eye’s retina. The value x indicates the intensity of the excitation of such a cell; let us say that
- x=1 if the cell perceives black and that
- x=0 if it perceives white
All X cells are connected by synapses – here w1 to w3– to what can be compared to an artificial neuron. The latter is capable of only one thing: to calculate x1×w1+x2×w2+x3×w3, in short :
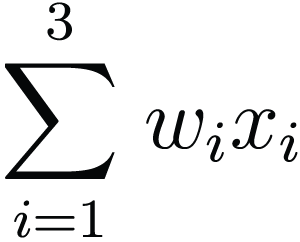
The last neuron in the network, Y represents the result of the calculation. Let us now assume that we want our smart grid to know the difference between a point (.) and a double point (:). To his three-cell retinal artificial eye, everything is in the form (x1,x2,x3). A point can take three forms: (1,0,0), (0,1,0) and (0,0,1). A double point will be (1,0,1), (0,1,1) or (1,1,0). Let us also define the initial values of W as w1 = 3, w2 = 1 and w3 = 2, or more simply, W=(3,1,2); it is customary to define these values randomly in the first step. What happens if I present a (1,0,0) to the machine? 1×3+0×1+0×2 = 3. A double point (0,1,1), on the other hand, gives 0×3+1×1+1×2 = 3; same result! The machine is unable to differentiate “.” of “:” That’s where the training comes in. It consists in changing the synaptic weights W – comparable to the thickness of the brain’s synapses or their electrochemical conductivity – until the machine can differentiate. Let’s change them, then. Let’s say that W=(1,1,1); the result improves. By submitting (1,0,0), I get 1. By submitting (0,1,1), I get 2. The same applies for (1,0,1) → 2 and (0,1,0) → 1 etc. The machine knows how to say if it sees a “.” of “:”.
Let us now consider that even a box jellyfish has not 3, but 24 photoreceptive cells. It takes a hundred such cells, and twenty neurons, to distinguish all the letters of the alphabet; even more to assign the image of a face to a person. Neuromimetic networks often have hundreds of neurons, which are arranged in successive layers by deep learning enthusiasts. Artificial intelligence is also not limited to image recognition; a video (Aradhye, Toderici, & Yagnik, 2009), text, melody or smell (Keller et al., 2017) can all be perceived as a vector (x1 … xn). Finally, the synaptic weights do not adapt randomly, but by a procedure that takes into account the magnitude of the machine’s errors at each consecutive training phase.
The training itself, nevertheless, remains focalized on the difference between true and false, 0 and 1, which already preoccupied ancient logic: is this facial expression sad? is this sentence obscene? If the automaton misunderstands, let it change its synaptic weights! Artificial intelligence remains a code of law, a decision-making tool: should we invest in this startup? Should this tweet be deleted? This intelligence, like Sumerian writing in its early days, still has to emancipate itself from its goals to become a creative intelligence.
Artificial intelligence as a way to think, together, what we are unable to think for ourselves
What already exists are unsupervised networks, which find forms and regularities in data sets without postulating on their possible “truth”. There are also generative networks, such as the one trained by the artist Robbie Barratt. Trained from hundreds of realistic paintings, his algorithm generates others, more evocative of the works of Max Ernst or Francis Bacon, who often used collage or inspired themselves from photography. Both can be regarded as a network node, an open individual synthesizing hundreds of creations from various sources. The interest of artificial intelligence is precisely its capacity for super-human synthesis; as a tool for the collective author; as a tool to think, together, what we are unable to think for ourselves; as a means of creating works in which the interpreter will no longer seek the embarrassing auto-fiction of an individual but the consciousness of a civilization. Unless, of course, we leave this tool in hands of Tay, Microsoft’s infamous chatbot that became abject in less than a day when she learned from the hateful blabber of less inspired inhabitants of the social media.
Reference note
This text is a translation of the French original “Entre l’art et la vérité“, in La Cinquième Saison: Revue littéraire romande, volume 6, ‘Portrait des robots’. 2019.
The dossier ‘Portrait des robots’ of the 6th volume of La Cinquième Saison also contains controbutions by François Rouiller, Serge Thorimbert, Daniela Cerqui, Olivier Sillig, Agnès Giard, Nicolas Alucq, Marc Attalah, Dominique Bourg, Anthony Vallat and Colin Palish.
In the meantime, I’ve written a book on the subject: Ourednik, A. (2021). Robopoïèses. Les intelligences artifcielles de la nature. La Baconnière.
Further reading
Aradhye, H., Toderici, G., & Yagnik, J. (2009). Video2text: Learning to annotate video content. In Data Mining Workshops, 2009. ICDMW’09. IEEE International Conference on (p. 144–151). IEEE.
Clarke, A. C. (1968). 2001: A Space Odyssey. UK: Hutchinson.
Kak, S. (2005). Aristotle and Gautama on Logic and Physics.
Keller, A., Gerkin, R. C., Guan, Y., Dhurandhar, A., Turu, G., Szalai, B., … Meyer, P. (2017). Predicting human olfactory perception from chemical features of odor molecules. Science, 355(6327), 820‑826.
Vidyabhusana, S. C. (1920). A History of Indian Logic: Ancient, Mediaeval and Modern Schools. Motilal Banarsidass Publishe.
Wolf, B. (2016). Kafka in Habsburg. Mythen und Effekte der Bürokratie. Administory. Zeitschrift für Verwaltungsgeschichte, 1(0).